Eine komplexe Zahl können wir als Punkt im $\mathbb{R}^2$ auffassen und somit auch als Vektor betrachten. In dieser Blog-Folge zeige ich Dir, wie die arithmetischen Operationen für komplexe Zahlen geomtrisch im $\mathbb{R}^2$ dargestellt werden können.
Gaußsche Zahlenebene
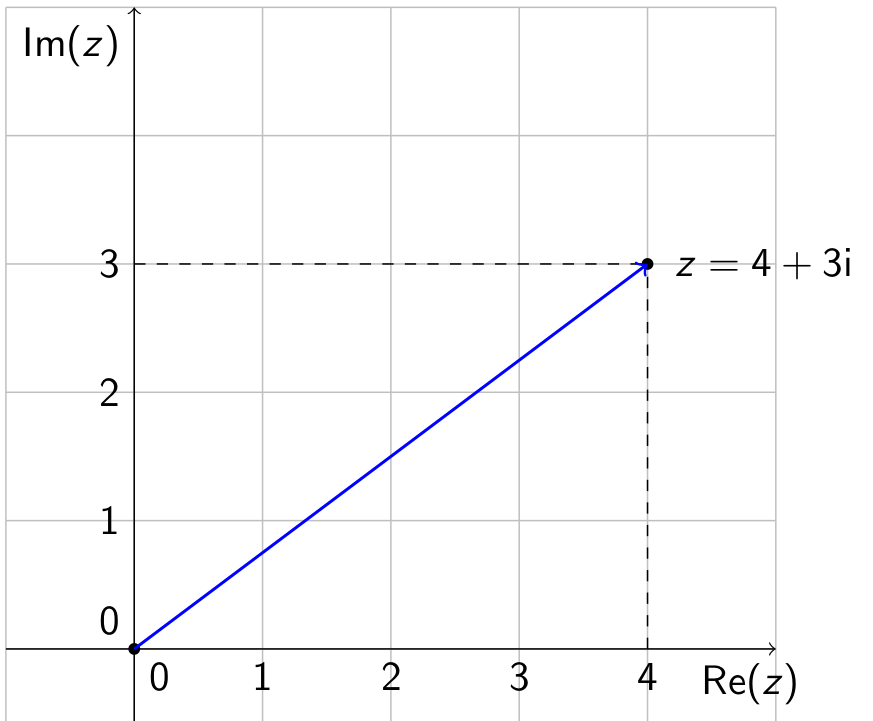
Wir hatten die Menge $\C$ der komplexen Zahlen als Paare von reellen Zahlen definiert. Diese Paare können wir als Punkte einer Ebene auffassen, die wir die gaußsche Zahlenebene nennen. Die gaußsche Zahlenebene versehen wir nun mit einem kartesischen Koordinatensystem, das von den beiden orthogonalen Vektoren $1$ und $i$ aufgespannt wird. Hierbei ist es üblich, den Realteil auf die waagerechte Achse zu legen und den Imaginärteil auf die senkrechte Achse. Eine komplexe Zahl $z=a + b\I$ hat dann die horizontale Koordinate $a$ und die vertikale Koordinate $b$.
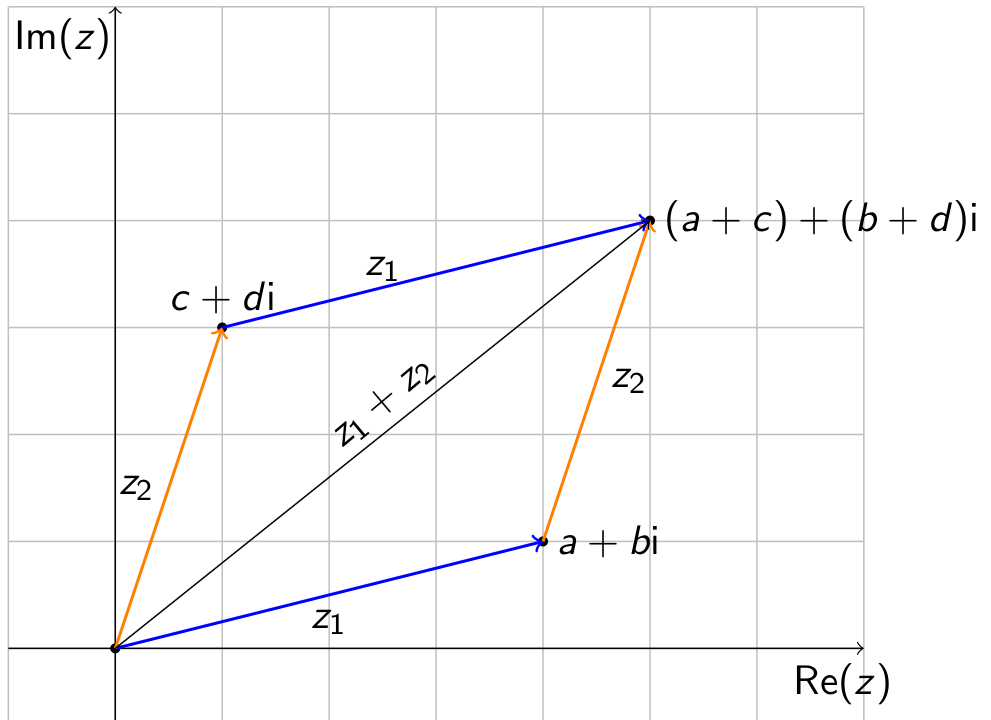
Die Addition zweier komplexer Zahlen erfolgt komponentenweise: Realteil plus Realteil und Imaginärteil plus Imaginärteil. Damit entspricht sie der üblichen Vektoraddition im Vektorraum $\R^2$, wobei wir die Punkte in der gaußschen Zahlenebene mit ihren Ortsvektoren assoziieren.
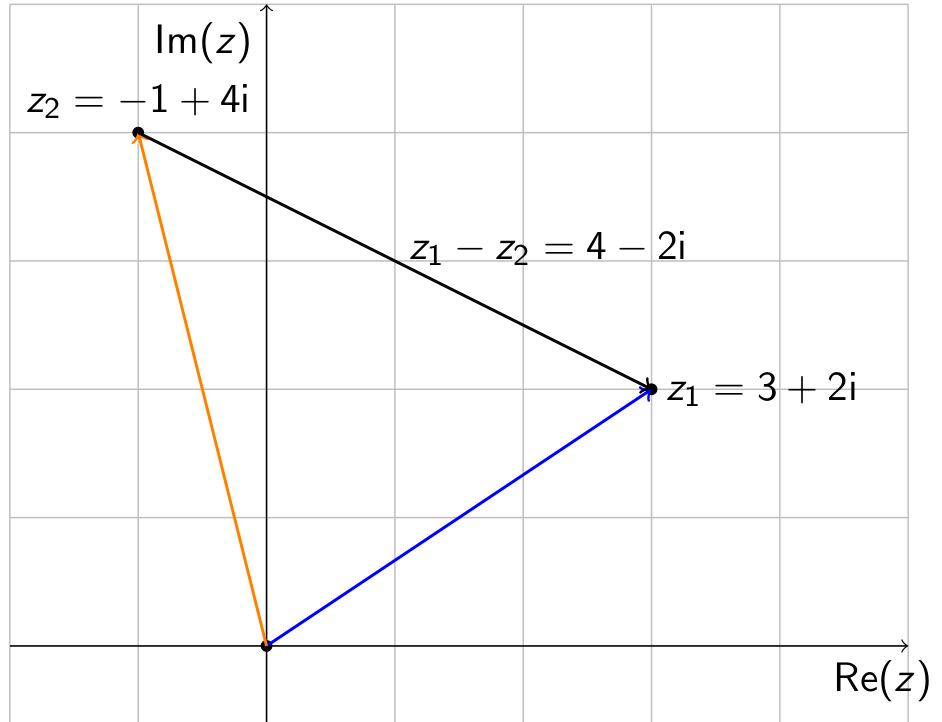
Die Subtraktion zweier komplexer Zahlen entspricht dann auch der Vektorsubtraktion im $\R^2$.
Polarkoordinaten
Neben der Möglichkeit, die Lage einer komplexen Zahl in der gaußschen Zahlenebene durch Real- und Imaginärteilkoordinate zu beschreiben, gibt es noch eine weitere: sogenannte Polarkoordinaten.
Früher, als alles noch besser war, auch die Mathematikausbildung an den Schulen, hat man Polarkoordinaten in der Mittelstufe immer durchgenommen. Heute ist dies leider nicht mehr der Fall. Wenn ich meine Studenten frage, ob sie schon mal etwas von Polarkoordinaten gehört haben, dann kann ich deutlich die Fragezeichen in ihren Gesichtern sehen.
Solltest Du Polarkoordinaten schon kennen, dann kannst Du diesen Abschnitt überspringen. Wenn nicht, dann lerne jetzt, was Polarkoordinaten sind. Du kannst sie allgemein in der Ebene verwenden, nicht nur für komplexe Zahlen. Wir benötigen sie in dieser Blog-Folge für die anschauliche Interpretation der Multiplikation von komplexen Zahlen. Mit Polarkoordinaten sieht man nämlich sehr schön, was bei der Multiplikation genau passiert.
Polarkoordinaten für eine komplexe Zahl $z=a+b\I$ bestehen aus zwei Teilen:
-
einer reellen Zahl $r \geq 0$, die den Abstand von $z$ zum Ursprung angibt und
-
einem Winkel $\varphi$, der die Richtung angibt, in die die Zahl $z$ vom Ursprung aus gesehen liegt.
Du kannst die Polarkoordinaten dann folgendermaßen interpretieren: Die Zahl, die vom Urprung aus gesehen in Richtung $\varphi$ in einer Entfernung von $r$ Längeneinheiten liegt, ist die Zahl $z$. So kann man jeden Punkt der gaußschen Zahlenebene eindeutig beschreiben. Zum Beispiel hat die komplexe Zahl $3 + 3\I$ die Polarkoordinatendarstellung $(r,\varphi) = (\sqrt{18}, 45^\circ)$. Die nachfolgende Grafik verdeutlich dies.
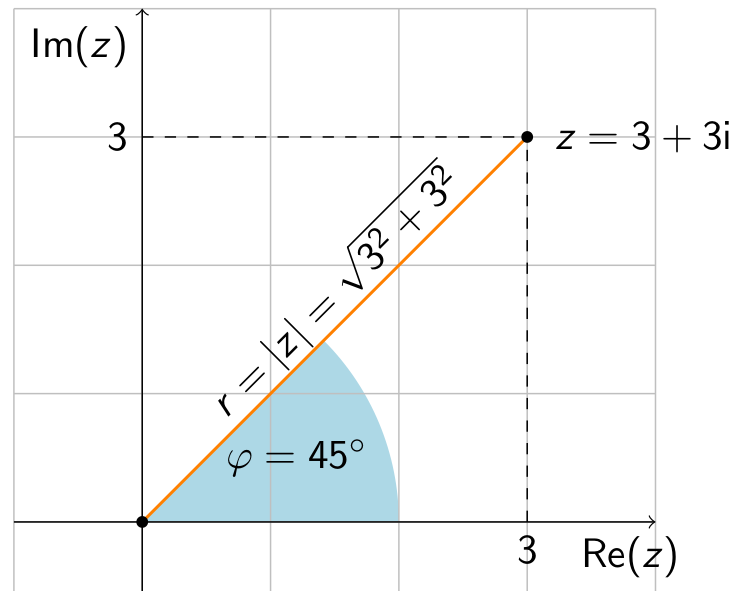
An der Grafik siehst Du auch, wie die Richtungsangabe zu interpretieren ist. Der Winkel $\varphi$ gibt den Winkel an, den die Realteilachse (in positive Richtung) mit dem Strahl bildet, der vom Ursprung aus durch $z$ verläuft. Dabei entsteht ein positiver Winkel, wenn wir die Realteilachse gegen den Uhrzeigersinn drehen müssen, um auf den Strahl zu treffen.
Für uns wird wichtig sein, wie wir die Koordinatendarstellungen zwischen der Darstellung $z=a + b\I$ und den Polarkoordinaten $(r,\varphi)$ umrechnen können. Dies behandeln wir um übernächsten Abschnitt. Vorher möchte ich noch darauf eingehen, in welcher Einheit wir Winkel in der Mathematik und der Informatik angeben.
Bogenmaß
In den mathematisch orientierten Wissenschaften wie der Informatik geben wir Winkel nicht in der Einheit Grad an, sondern im Bogenmaß mit der Einheit Radiant. Um zu verstehen, worin der Unterschied besteht, schauen wir uns den Einheitskreis an, also den Kreis um den Ursprung mit Radius $1$.
Wenn wir irgendeinen Punkt $z$ auf dem Einheitskreis betrachten, dann bildet der Strahl, der im Ursprung beginnt und durch $z$ geht, einen Winkel mit der Realteilachse. Wir können also jedem Punkt $z$ auf dem Einheitskreis eindeutig einen Winkel $\varphi$ zuordnen. Ebenso gehört zu jedem Winkel zwischen $0^\circ$ (inklusive) und $360^\circ$ (exklusive) ein eindeutiger Punkt auf dem Einheitskreis. Damit haben wir eine bijektive Abbildung zwischen Winkeln und Punkten auf dem Einheitskreis.
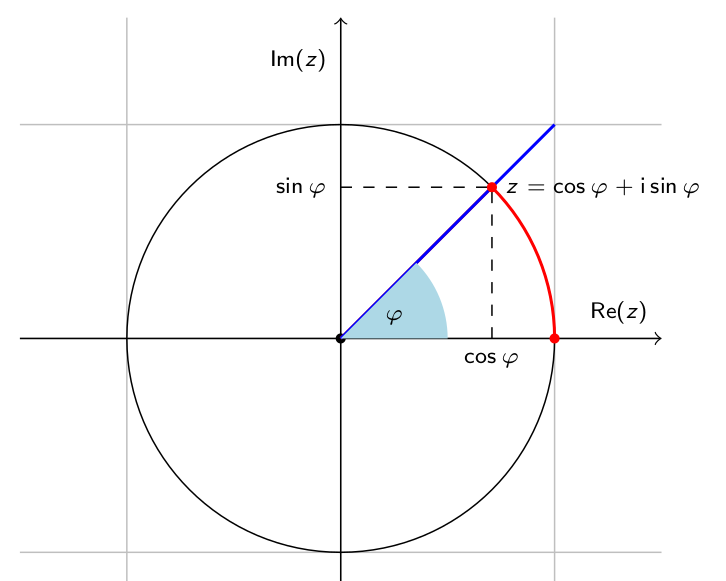
Als nächstes machen wir uns klar, dass wir die Lage eines Punktes auf dem Einheitskreis auch durch die Länge des Kreisbogens beschreiben können, der von $(1,0)$ aus in mathematisch positiver Richtung (gegen den Uhrzeigersinn) bis zum fraglichen Punkt $z$ verläuft (die rote Linie in der Grafik). Einmal komplett um den Kreis herum würde einem Winkel von $360^\circ$ entsprechen und somit einer Bogenlänge von $2\pi$, dem Umfang des Einheitskreises. Alle anderen Winkel können wir anteilig umrechnen. So gehört beispielsweise zu $90^\circ$ die Bogenlänge eines Viertelkreises, also $\frac{\pi}{2}$. Damit können wir jedem Winkel zwischen $0^\circ$ und $360^\circ$ (Einheit Grad) eineindeutig einen Wert zwischen $0$ und $2\pi$ (Einheit Radiant) zuordnen.
Wenn Du in der Softwareentwicklung mathematische Funktionen für Winkelberechnungen nutzen willst, musst Du die Winkel immer im Bogenmaß, also mit der Einheit Radiant, angegeben. Winkelangaben in Grad verstehen solche Funktionen nicht. Mit den folgenden Formeln kannst Du Winkel zwischen Grad und Radiant einfach umrechnen: \[ \text{Winkel in Grad} = \text{Winkel in Radiant} \cdot \frac{180}{\pi} \] und somit \[ \text{Winkel in Radiant} = \text{Winkel in Grad} \cdot \frac{\pi}{180}. \]
Umrechnung zwischen den Koordinatendarstellungen
Schau Dir nochmals das Bild von oben mit dem Einheitskreis an. Für einen Punkt $z$ auf dem Einheitskreis, zu dem der Winkel $\varphi$ gehört, ist $\cos\varphi$ die Realteil- und $\sin\varphi$ die Imaginärteilkoordinate. Es gilt also \[ z = \cos\varphi + \I \sin\varphi. \] Beträgt die Entfernung einer Zahl $z\in\C$ vom Ursprung nun nicht $1$ sondern $r$, dann muss demnach \[ z = r \cdot (\cos\varphi + \I \sin\varphi) \] gelten. Statt dieser Schreibweise sieht man in Lehrbüchern aber auch häufig \[ z = r \e^{\I\varphi}. \] Was hat es damit auf sich? An dieser Stelle im Kurs haben wir weder die Zahl $\e$ definiert, noch die komplexe Exponentialfunktion $f(z) = \e^z$ eingeführt. Aber im Verlauf dieses Kurses werden wir all diese Definitionen kennenlernen. Wir werden dann auch sehen, dass die komplexe Zahl $\e^{i\varphi}$ für $\varphi\in\R$ immer auf dem Einheitskreis liegt, d. h. es gilt stets \[ \left|\e^{\I\varphi}\right| = 1. \] Tatsächlich ist der Term $\e^{\I\varphi}$ nur eine andere Schreibweise für $\cos\varphi + \I \sin\varphi$. Somit gilt dann auch \[ r\e^{\I\varphi} = r \cos(\varphi) + \I\,r \sin(\varphi). \]
Wie rechnen wir zwischen den verschiedenen Koordinatendarstellungen hin und her? In eine Richtung ist dies ganz einfach. Wenn wir die Polarkoordinatendarstellung für eine komplexe Zahl $z$ haben, also $r$ und $\varphi$ kennen, dann muss ja, wie oben schon erwähnt, \[ z = r\cos(\varphi) + \I\,r\sin(\varphi) \] gelten, d. h. \[ \Re(z) = r \cos\varphi \] und \[ \Im(z) = r \sin\varphi. \] Wir können also die Real- und Imaginärteilkoordinaten einfach ermitteln, indem wir die Cosinus- bzw. die Sinusfunktion anwenden und die Funktionswerte mit dem Faktor $r$ multiplizieren.
Schwieriger wird es, wenn wir $z$ in der Form $z = a + b\I$ gegeben haben und daraus die Polarkoordinatendarstellung, also $r$ und $\varphi$, ermitteln möchten. Zwar können wir $r$ leicht bestimmen, denn \[ r = |z| = \sqrt{a^2 + b^2}, \] aber um den Winkel $\varphi$ zu ermitteln, der zu $a$ und $b$ gehört, müssen wir etwas mehr Aufwand betreiben. Für die Identität zweier komplexer Zahlen müssen Real- und Imaginärteil übereinstimmen, womit \[ a = r\cos(\varphi) \wedge b = r\sin(\varphi) \] und daraus wiederum \[ \cos(\varphi) = \frac{a}{r} \wedge \sin(\varphi) = \frac{b}{r} \] folgt. Eine weitere trigonometrische Funktion ist der Tangens, definiert als Quotient von Sinus und Cosinus: \[ \tan(\varphi) = \frac{\sin(\varphi)}{\cos(\varphi)}. \] Damit erhalten wir die Gleichung \[ \tan(\varphi) = \frac{\frac{b}{r}}{\frac{a}{r}} = \frac{b}{a}. \] Diese Gleichung müssen wir jetzt nach $\varphi$ auflösen, wofür wir die Umkehrfunktion des Tangens, den Arcustangens, nutzen. Es ergibt sich \[ \varphi = \arctan\left(\frac{b}{a}\right). \] Klingt jetzt gar nicht so schwer, oder? Leider ist dies aber nur die halbe Wahrheit. Erstens ist der Bruch $\frac{b}{a}$ für $a=0$ nicht definiert und zweitens ist der Tangens auf seinem Definitionsbereich keine bijektive Funktion.
Die erste Schwierigkeit können wir recht schnell beseitigen. Gilt $a=0$, dann liegt die komplexe Zahl $z$ als Punkt in der gaußschen Zahlenebene auf der Imaginärteilachse. Damit gilt für den Winkel $\varphi$ entweder $\varphi = \frac{\pi}{2}$, nämlich genau dann wenn $b$ positiv ist, oder $\varphi = \frac{3\pi}{2}$, falls $b$ negativ ist.
Um den Arcustangens, die Umkehrfunktion des Tangens, bilden zu können, müssen wir uns auf eine Teilmenge des Definitionsbereichs beschränken, in dem der Tangens bijektiv ist. Hierzu nutzt man den Bereich zwischen $-\frac{\pi}{2}$ und $\frac{\pi}{2}$. Damit gilt: \[ \arctan: \R \rightarrow (-\frac{\pi}{2},\frac{\pi}{2}), \] d. h. der Arcustangens bildet eine beliebige reelle Zahl auf einen Winkel zwischen $-90^\circ$ und $90^\circ$ ab. In der gaußschen Zahlenebene sind dies der erste und vierte Quadrant, also der Teil der Ebene, für den $a> 0$ gilt. Daher können wir die oben hergeleitete Formel $\varphi = \arctan\left(\frac{b}{a}\right)$ für $a> 0$ bedenkenlos anwenden.
Im Fall von $a <0$ liegt $z$ im zweiten oder dritten Quadranten der gaußschen Zahlenebene. Für den Winkel $\varphi$ der Polarkoordinatendarstellung von $z$ gilt dann $\frac{\pi}{2} < \varphi < \frac{3\pi}{2}$. Damit liegt $\varphi$ außerhalb des Bildbereichs des Arcustangens. Die Formel $\varphi = \arctan\left(\frac{b}{a}\right)$ liefert demnach für diesen Fall nicht den korrekten Winkel.
Glücklicherweise gilt für den Tangens aber \[ \tan(\varphi) = \tan(\varphi+\pi). \] Deshalb müssen wir im Fall von $a <0$ einfach nur den Winkel $\pi$ zum Ergebnis des Arcustangens addieren. Damit erhalten wir insgesamt folgende Berechnungsvorschrift für den Winkel $\varphi$ einer komplexen Zahl $z=a + b\I$: \[ \varphi = \left\{ \begin{array}{rl} \frac{\pi}{2} & \text{für } a = 0 \wedge b > 0 \\ \frac{3\pi}{2} & \text{für } a = 0 \wedge b < 0 \\ \arctan\left(\frac{b}{a}\right) & \text{für } a > 0 \\ \pi + \arctan\left(\frac{b}{a}\right) & \text{für } a < 0 \end{array} \right. \] Vielleicht ist Dir aufgefallen, dass diese Berechnungsvorschrift den Fall $a=b=0$ nicht abdeckt. Dies ist aber kein Problem, denn für $a=b=0$ gilt $z=0$ und damit auch $r = |z| = 0$. Schon damit können wir die $0$ in Polarkoordinaten eindeutig identifizieren.
In der Literatur findest Du für die Berechnung des Winkels $\phi$ häufig die Bezeichnung $\varphi = \text{arg}(z)$. Die Funktion $\text{arg}(z)$ wird als das Hauptargument von $z$ bezeichnet. Im Unterschied zu unserer Formel von oben wird das Hauptargument so definiert, dass ein Winkel $\varphi$ mit $-\pi < \varphi \leq \pi$ entsteht. Eine Formel hierfür ist \[ \varphi = \text{arg}(z) := \left\{ \begin{array}{rl} \arctan\left(\frac{b}{a}\right) & \text{für } a > 0 \\ \arctan\left(\frac{b}{a}\right) + \pi & \text{für } a < 0 \wedge b \geq 0 \\ \arctan\left(\frac{b}{a}\right) - \pi & \text{für } a < 0 \wedge b < 0 \\ \frac{\pi}{2} & \text{für } a = 0 \wedge b > 0 \\ -\frac{\pi}{2} & \text{für } a = 0 \wedge b < 0. \end{array} \right. \] Diese Formel ist äquivalent zu der Formel von oben. Für $\varphi$ entstehen die gleichen Winkel, nur eventuell anders formuliert, z. B. als $-\frac{\pi}{2}$ statt $\frac{3\pi}{2}$.
Für solche Umrechnungen, für eine Klausur, die ohne Taschenrechner geschrieben wird und überhaupt für den Umgang mit trigonometrischen Funktionen solltest Du die wichtigsten Werte für Sinus und Cosinus auswendig kennen. Die folgende Tabelle zeigt Dir diese Werte inklusive die des Tangens.
| $\varphi$ in Radiant | $0$ | $\frac{\pi}{6}$ | $\frac{\pi}{4}$ | $\frac{\pi}{3}$ | $\frac{\pi}{2}$ |
|---|---|---|---|---|---|
| $\varphi$ in Grad | $0^\circ$ | $30^\circ$ | $45^\circ$ | $60^\circ$ | $90^\circ$ |
| $\sin\varphi$ | $0$ | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ | $1$ |
| $\cos\varphi$ | $1$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | $0$ |
| $\tan\varphi$ | $0$ | $\frac{1}{\sqrt{3}}$ | $1$ | $\sqrt{3}$ | $-$ |
Aus den Werten dieser Tabelle kannst Du die Werte für andere Winkel wie $120^\circ, 135^\circ, 150^\circ$ usw. durch Spiegelung an den Achsen leicht herleiten. Beispielsweise wird der Punkt auf dem Einheitskreis für $30^\circ$ durch Spiegelung an der Imaginärteilachse auf den Punkt für $150^\circ$, dies entspricht $\frac{5\pi}{6}$, abgebildet. Damit bleibt der Sinus identisch, aber der Cosinus wechselt das Vorzeichen. Also: \[ \sin\left(\frac{5\pi}{6}\right) = \frac{1}{2} \quad\text{und}\quad \cos\left(\frac{5\pi}{6}\right) = - \frac{\sqrt{3}}{2}. \]
Beachte, dass der Tangens für $\frac{\pi}{2}$ und dementsprechend auch für $\frac{3\pi}{2}$ nicht definiert ist, weil der Cosinus an diesen Stellen den Wert $0$ hat.
Übung 1
Gebe für die folgenden komplexen Zahlen in Polarkoordinatendarstellung jeweils die Darstellung in der Form $a + b\I$ an.
$z = 5 \e^{\I \frac{\pi}{6}}$
$z = 3 \e^{\I \frac{3\pi}{2}}$
$z = 4 \e^{\I \frac{5\pi}{6}}$
$z = 7 \e^{-\I \pi}$
-
Die Werte für Cosinus und Sinus des Winkels $\varphi = \frac{\pi}{6}$ können wir der obigen Tabelle entnehmen. Damit erhalten wir \[ z = 5\e^{\I \frac{\pi}{6}} = 5 (\cos(\frac{\pi}{6}) + \I\,\sin(\frac{\pi}{6})) = 5(\frac{\sqrt{3}}{2} + \I\,\frac{1}{2}) = \frac{5\sqrt{3}}{2} + \frac{5}{2}\I. \]
-
Der Winkel $\varphi = \frac{3}{2}\pi$ entspricht $270^\circ$, also einem Dreiviertelkreis. Damit gilt \[ \cos(\frac{3}{2}\pi) = 0 \quad\text{und}\quad \sin(\frac{3}{2}\pi) = -1. \] Also: \[ z = 3 \e^{\I \frac{3\pi}{2}} = 3(0 - \I) = -3\I. \]
-
Der Winkel $\varphi = \frac{5}{6}\pi$ entspricht $150^\circ$. Es gilt \[ \sin(\frac{5}{6}\pi) = \sin(\frac{1}{6}\pi) = \frac{1}{2} \] und \[ \cos(\frac{5}{6}\pi) = - \cos(\frac{1}{6}\pi) = - \frac{\sqrt{3}}{2}. \] Also: \[ z = 4 \e^{\I\frac{5\pi}{6}} = 4(-\frac{\sqrt{3}}{2} + \frac{\I}{2}) = -2\sqrt{3} + 2\I. \]
-
Der Winkel $\varphi = -\pi$ entspricht $-180^\circ$ was aber wiederum $180^\circ$ also $\pi$ entspricht. Also: \[ z = 7\e^{-\I\pi} = 7(-1 + 0\I) = -7. \]
Übung 2
Gebe für die folgenden komplexen Zahlen $z = a + b\I$ ihre Polarkoordinatendarstellung an.
$z = 3\I$
$z = -5\I$
$z = 3\sqrt{3} + 3\I$
$z = -\frac{5}{\sqrt{2}} - \frac{5}{\sqrt{2}}\I$
$z = -7$
Wir nutzen stets die Formel für das Hauptargument $\text{arg}(z)$ (siehe oben).
-
Hier greift der vierte Fall aus der Formel für das Hauptargument, denn es gilt $a=0$ (Realteil) und $b=3 > 0$ (Imaginärteil). Wir erhalten somit \[ z = 3\I = 3\e^{\I\frac{\pi}{2}}. \]
-
Wegen $a=0$ und $b=-5 < 0$ nutzen wir hier den fünften Fall aus der Formel des Hauptarguments. Wir erhalten \[ z = -5\I = -5\e^{-\I\frac{\pi}{2}}. \] Da der Winkel $-\frac{\pi}{2}$ dem Winkel $\frac{3\pi}{2}$ entspricht, gilt auch \[ z = -5\e^{\I\frac{3\pi}{2}}. \]
-
Hier ist der Realteil $a=3\sqrt{3}$ positiv. Damit greift der erste Fall aus der Formel für das Hauptargument. Zunächst gilt \[ \frac{b}{a} = \frac{3}{3\sqrt{3}} = \frac{1}{\sqrt{3}}. \] Jetzt müssen wir schauen, für welchen Winkel der Tangens den Wert $\frac{1}{\sqrt{3}}$ annimmt. Gemäß der Tabelle oben ist dies bei $\frac{\pi}{6}$ der Fall. Also gilt \[ \varphi = \arctan(\frac{b}{a}) = \arctan(\frac{1}{\sqrt{3}}) = \frac{\pi}{6}. \] Weiterhin gilt \[ |z| = \sqrt{9\cdot 3 + 9} = \sqrt{36} = 6. \] und somit \[ z = 6 \e^{\I\frac{\pi}{6}}. \]
-
Es gilt $a = b =-\frac{5}{\sqrt{2}}$, womit beide Teile negativ sind. Damit müssen wir den dritten Fall aus der Formel für das Hauptargument nutzen. Es ergibt sich \[ \varphi = \arctan(\frac{b}{a}) - \pi = \arctan(1) - \pi = \frac{\pi}{4} - \pi = -\frac{3\pi}{4}. \] Weiterhin gilt \[ |z| = \sqrt{\frac{25}{2} + \frac{25}{2}} = \sqrt{\frac{50}{2}} = \sqrt{25} = 5 \] und somit \[ z = 5 \e^{-\I\frac{3\pi}{4}}. \]
-
Wegen $a= -7 < 0$ und $b=0$ nutzen wir den zweiten Fall aus der Formel für das Hauptargument. Es ergibt sich \[ \varphi = \arctan(\frac{b}{a}) + \pi = \arctan(0) + \pi = 0 + \pi = \pi. \] Außerdem gilt $|z| = 7$ und somit \[ z = 7 \e^{\I \pi}. \]
Hinweis: Es gilt \[ 7 \e^{\I \pi} = 7 \e^{-\I \pi}, \] denn der Winkel $\pi$ entspricht $180^\circ$, was aber wiederum $-180^\circ$ und somit $-\pi$ entspricht. Damit ist \[ z = 7 \e^{-\I \pi} \] ebenfalls eine korrkete Polarkoordinatendarstellung von $z=-7$ (vgl. die letzte Aufgabe von Übung 1).
Multiplikation
Mit der Polarkoordinatendarstellung können wir die Multiplikation zweier komplexer Zahlen sehr anschaulich darstellen.
Es sei $z_1 = r \e^{\I \varphi}$ und $z_2 = s \e^{\I \psi}$. Dann ergibt sich für das Produkt: \[ z_1 \cdot z_2 = r \e^{\I \varphi} s \e^{\I \psi} = rs\,\e^{\I(\varphi + \psi)}. \] Damit ist der Winkel, der zum Produkt der beiden Zahlen gehört, die Summe der einzelnen Winkel und die Entfernung vom Ursprung ist das Produkt der einzelnen Entfernungen. Die nachfolgende Grafik veranschaulicht dies beispielhaft.
Damit wird uns auch schnell klar, wie das multiplikativ Inverse einer komplexen Zahl $z = r\e^{\I\varphi}$ aussehen muss. Da bei der Multiplikation Winkel addiert werden, und die $1$ den Winkel $0$ hat, muss $z^{-1}$ den Winkel $-\varphi$ aufweisen. Diesen Winkel erhalten wir aber genau für $\overline{z}$, dem konjugiert Komplexen von $z$. Dies können wir auch wieder gut der folgenden Graphik entnehmen.
Damit ist anschaulich klar, dass \[ z \,\overline{z} \in \R \] gelten muss. Da natürlich auch $|z| = |\overline{z}|$ gilt, können wir das Ergebnis von $z \,\overline{z}$ direkt angeben: \[ z \,\overline{z} = |z|^2 = \Re(z)^2 + \Im(z)^2, \] eine Formel, die wir schon aus der vorangegangenen Blog-Folge kennen. Mit dem Verständnis der geometrischen Hintergründe kannst Du Dir die Formel aber vermutlich viel leichter merken. Ebenso auch die Formel \[ z^{-1} = \frac{\overline{z}}{|z|^2}, \] denn sie folgt unmittelbar aus der Formel von oben.
Und wie können wir jetzt die Division zweier komplexer Zahlen $z_1$ und $z_2$ geometrisch interpretieren. Nun, die Division ist ja nicht anderes als die Multiplikation von $z_1$ mit dem multiplikativ Inversen $z_2^{-1}$ der zweiten Zahl. Wir hatten soeben gesehen, dass für die Bildung von $z_2^{-1}$ das Vorzeichen des Winkels von $z_2$ vertauscht wird. Also wird bei der Division die Differenz der beiden Winkel gebildet und die Entfernungen werden dividiert.
Potenzen
Für eine komplexe Zahl in Polarkoordinaten können wir die $n$-te Potenz recht einfach bestimmen: \begin{eqnarray*} & & z = r\e^{\I\varphi} = r\cdot(\cos\varphi + \I \sin\varphi) \\ & \Longrightarrow & z^n = \left(r\e^{\I\varphi}\right)^n = r^n \e^{\I n \varphi} = r^n\cdot(\cos(n\varphi) + \I\sin(n\varphi)). \end{eqnarray*} Demnach bilden wir die $n$-te Potenz, indem wir den zu $z$ gehörenden Winkel mit $n$ multiplizieren und den Abstand $r$ mit $n$ potenzieren.
Beispiel
Es sei $z = \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} \I$. Was ergibt sich für $z^{2024}$? Klingt zunächst sehr schwierig. Aber: \[ |z| = \sqrt{\left(\frac{\sqrt{2}}{2}\right)^2 + \left(\frac{\sqrt{2}}{2}\right)^2} = \sqrt{\frac{1}{2} + \frac{1}{2}} = 1 \] und \[ \varphi = \arctan\left( \frac{ \frac{\sqrt{2}}{2} }{ \frac{\sqrt{2}}{2} } \right) = \arctan(1) = \frac{\pi}{4}. \] Also gilt \[ z = \e^{\frac{\pi}{4}\I} \] und damit \[ z^{2024} = \left(\e^{\frac{\pi}{4}\I}\right)^{2024} = \e^{2024 \frac{\pi}{4}\I} = \e^{506\pi\I} = \e^{253 \cdot 2\pi\I} = \left(\e^{2\pi\I}\right)^{253} = 1^{253} = 1. \]Wurzeln
Und wie ziehen wir nun eine Wurzel aus einer komplexen Zahl $z$? Nun, $\sqrt{z}$ ist eine Zahl, die mit sich selbst multipliziert wieder $z$ ergibt. Wir haben gesehen, dass die Multiplikation einer Addition der Winkel in Polarkoordinatendarstellung entspricht. Wenn also $z$ den Winkel $\varphi$ hat, muss $\sqrt{z}$ den Winkel $\frac{\varphi}{2}$ haben, denn $\frac{\varphi}{2} + \frac{\varphi}{2} = \varphi$. Damit ergibt sich: \begin{eqnarray*} & & z = r \cdot (\cos\varphi + \I \sin\varphi) \\ & \Longrightarrow & \sqrt{z} = \sqrt{r} \cdot (\cos\frac{\varphi}{2} + \I\sin\frac{\varphi}{2}) \end{eqnarray*} Diese Erkenntnis nutzen wir im nächsten Beispiel, um $\sqrt{\I}$ zu ermitteln.
Beispiel
Es gilt \[ \I = \cos\frac{\pi}{2} + \I \sin\frac{\pi}{2} \] und $|\I| = 1$. Damit erhalten wir \begin{eqnarray*} \sqrt{\I} & = & \cos\frac{\pi}{4} + \I \sin\frac{\pi}{4} \\ & = & \frac{\sqrt{2}}{2} + \I \frac{\sqrt{2}}{2} \\ & = & \frac{\sqrt{2}}{2}(1 + \I). \end{eqnarray*} Du hast Zweifel, dass dies richtig ist? Kein Problem, lass uns die Probe machen! Ein Ergebnis zu überprüfen ist immer gut.
Probe: \begin{eqnarray*} \left( \frac{\sqrt{2}}{2}(1 + \I) \right)^2 & = & \frac{1}{2}(1+\I)^2 \\ & = & \frac{1}{2}(1^2 + 2\I + \I^2) \\ & = & \frac{1}{2}(1 + 2\I -1) \\ & = & \frac{2\I}{2} \\ & = & \I. \end{eqnarray*} Also $\frac{\sqrt{2}}{2}(1 + \I)$ tatsächlich eine Wurzel von $\I$.
Ich habe am Ende des letzen Beispiels ganz bewusst von "einer" statt von "der" Wurzel gesprochen. In den reellen Zahlen haben wir $\sqrt{a}$ also die eindeutige positive Lösung der Gleichung $x^2 = a$ definiert. Da die komplexen Zahlen aber ja keinen angeordneten Körper bilden, gibt es auch keine positiven komplexen Zahlen. Jede Lösung der Gleichung $z^2 = a$ ist nun gleichberechtigt. Daher können wir nicht von "der" Wurzel sprechen.
So hatten wir oben $\frac{\sqrt{2}}{2}(1 + \I)$ als eine Wurzel von $\I$ ermittelt. Die Gleichung $z^2 = \I$ wird aber natürlich auch von \[ z = -\frac{\sqrt{2}}{2}(1 + \I) \] gelöst. Dementsprechend hat $\I$ nicht nur eine sondern zwei Wurzeln.
Diesen Gedanken möchte ich nun noch etwas vertiefen, indem wir einmal die dritten Wurzeln von $\I$ berechnen. Wir wissen \[ \I = \cos\frac{\pi}{2} + \I \sin\frac{\pi}{2} = \e^{\I\frac{\pi}{2}}. \] Mit den Winkelkonstruktion solltest Du ja jetzt vertraut sein, so dass Dir schnell klar wird, dass \[ \sqrt[3]{\I} = \e^{\I\frac{\pi}{6}} = \cos\frac{\pi}{6} + \sin\frac{\pi}{6} = \frac{\sqrt{3}}{2} + \I \frac{1}{2} \] gelten muss. Damit kennen wir eine dritte Wurzel. Gibt es weitere und wenn ja, wie sehen sie aus?
Die Idee zur Berechnung weiterer Wurzeln ist die folgende: Statt den Winkel $\frac{\pi}{2}$ zu dritteln, was wir oben gemacht haben, könnten wir ja auch den Winkel $\frac{\pi}{2} + 2\pi$ dritteln, denn beide Winkel geben die gleiche Richtung an, nur anders formuliert: $\frac{\pi}{2}$ entspricht $90^\circ$, der Winkel $\frac{\pi}{2} + 2\pi$ dagegen $450^\circ$. Wir laufen also einmal zusätzlich um den Kreis.
Es gilt \[ \frac{\frac{\pi}{2} + 2\pi}{3} = \frac{5}{6}\pi. \] Damit haben wir eine weitere dritte Wurzel von $\I$ gefunden. \[ \sqrt[3]{\I} = \e^{\I\frac{5\pi}{6}} = \cos\frac{5\pi}{6} + \sin\frac{5\pi}{6} = -\frac{\sqrt{3}}{2} + \I \frac{1}{2}. \]
Dieses Spiel können wir natürlich weiter treiben. Warum nur einmal zusätzlich um den Kreis laufen und nicht zweimal? Zwei zusätzliche Kreise entsprechen dem Winkel $\frac{\pi}{2} + 4\pi$, also $810^\circ$. Wenn wir diesen Winkel dritteln, erhalten wir \[ \frac{\frac{\pi}{2} + 4\pi}{3} = \frac{3}{2}\pi. \] Nun gilt \[ \e^{\frac{3\pi}{2}} = -\I, \] wie wir leicht feststellen können, wenn wir auf den Einheitskreis schauen, denn $\frac{3\pi}{2}$ entspricht einem Winkel von $270^\circ$. Also: \[ \sqrt[3]{\I} = -\I. \] Hier fällt uns die Probe leicht: \[ (-\I)^3 = (-\I)^2(-\I) = \I^2 (-\I) = -(-\I) = \I. \]
Gibt es darüber hinaus weitere dritte Wurzeln von $\I$? Nein! Denn \[ \frac{\frac{\pi}{2} + 6\pi}{3} = \frac{\pi}{6} + 2\pi. \] Wir erhalten also keinen zusätzlichen Winkel. Dies gilt analog auch für alle anderen Vielfachen von $2\pi$. Wenn wir die $k$-ten Wurzeln einer komplexen Zahl $z\neq 0$ bestimmen, erhalten wir immer genau $k$-verschiedene Wurzeln!
Die am Beispiel der dritten Wurzeln von $\I$ demonstrierten Methode zur Berechnung der $k$-ten Wurzeln können wir verallgemeinern, wie der folgende Satz zeigt.
Satz
Es sei $z = r\cdot(\cos\varphi + \I \sin\varphi) \neq 0$. Dann erfüllen die komplexen Zahlen \[ z_j = \sqrt[k]{r}\cdot \left( \cos\left(\frac{\varphi}{k} + \frac{2\pi j}{k}\right) + \I\sin\left(\frac{\varphi}{k} + \frac{2\pi j}{k}\right) \right) ,\quad j = 0,\ldots,k-1 \] die Gleichung $z_j^k = z$.
Die komplexen Zahlen $z_j$ aus dem letzten Satz sind also die $k$-ten Wurzeln von $z$.
Beispiel
Die folgende Grafik zeigt die fünften Wurzeln von $z=1 + \I \sqrt{3}$.
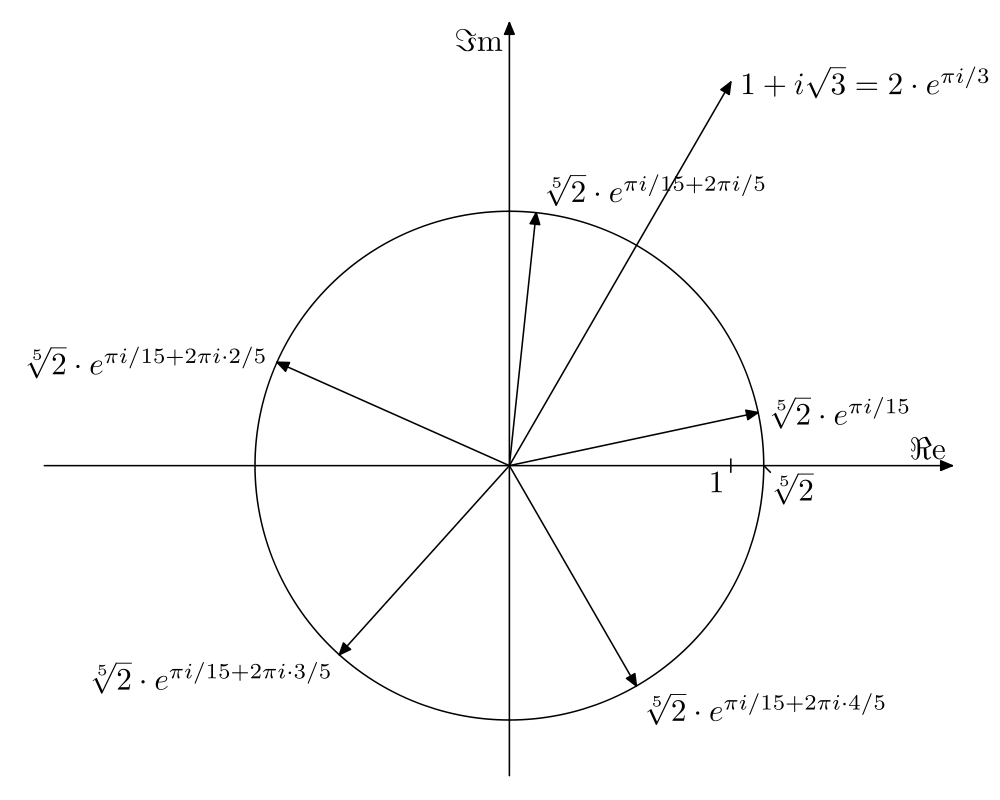
Für $z=1$ bezeichnen wir die $k$-ten Wurzeln als $k$-te Einheitswurzeln.
Übung
-
Wie lauten die vierten Einheitswurzeln?
-
Wie lauten die dritten Einheitswurzeln?
-
Wie lauten die achten Einheitswurzeln?
-
Wie lauten die sechsten Einheitswurzeln?
- $1, \I, -1, -\I$
- $1, -\frac{1}{2} + \frac{\sqrt{3}}{2}\I, -\frac{1}{2} - \frac{\sqrt{3}}{2}\I$
- $1, \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}\I, \I, -\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}\I, -1, -\frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2}\I, -\I, \frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2}\I$
- $1, \frac{1}{2} + \frac{\sqrt{3}}{2}\I, -\frac{1}{2} + \frac{\sqrt{3}}{2}\I, -1, -\frac{1}{2} - \frac{\sqrt{3}}{2}\I, \frac{1}{2} - \frac{\sqrt{3}}{2}\I$
Damit haben wir den Stoff des ersten Kapitels abgeschlossen. Es folgt noch eine Blog-Folge mit Übungen zu komplexen Zahlen, danach geht es mit der ersten Blog-Folge des zweiten Kapitels weiter.
Teilen und Drucken