Übungen zu Kapitel 1

1. $n=1$: \[ \sum_{k=1}^n (2k-1) = \sum_{k=1}^1 (2k-1) = 2\cdot 1 - 1 = 1 = 1^2 = n^2 \]

   $n \rightarrow n+1$: \begin{eqnarray*} \sum_{k=1}^{n+1} (2k-1) & = & (2(n+1)-1) + \sum_{k=1}^n (2k-1) \\[2mm] & \stackrel{I.V.}{=} & (2n+1)+n^2 \\[2mm] & = & n^2 + 2n + 1 \\[2mm] & = & (n+1)^2 \end{eqnarray*}

2. $n=1$: \[ \sum_{k=1}^n k^2 = \sum_{k=1}^1 k^2 = 1^2 = 1 = \frac{1(1+1)(2+1)}{6} = \frac{n(n+1)(2n+1)}{6} \]

   $n \rightarrow n+1$: \begin{eqnarray*} \sum_{k=1}^{n+1} k^2 & = & (n+1)^2 + \sum_{k=1}^n k^2 \\[2mm] & \stackrel{I.V.}{=} & (n+1)^2 + \frac{n(n+1)(2n+1)}{6} \\[2mm] & = & \frac{6(n+1)^2 + n(n+1)(2n+1)}{6} \\[2mm] & = & \frac{(n+1)(6(n+1) + n(2n+1))}{6} \\[2mm] & = & \frac{(n+1)(2n^2 + 7n + 6)}{6} \\[2mm] & = & \frac{(n+1)(n+2)(2n+3)}{6} \\[2mm] & = & \frac{(n+1)((n+1)+1)(2(n+1)+1)}{6} \end{eqnarray*}

3. $n=1$: \[ 8^n-1 = 8^1 - 1 = 8-1 = 7 \] und $7$ ist natürlich durch $7$ teilbar.

   $n \rightarrow n+1$: Es gilt \[ 8^{n+1} - 1 = 8\cdot 8^n -1 = (7+1)8^n - 1 = 7\cdot 8^n + 8^n - 1. \] Der Summand $7\cdot 8^n$ ist wegen der $7$ als Faktor durch $7$ teilbar, der Summand $8^n-1$ ist nach Induktionsvoraussetzung durch $7$ teilbar.

   Also ist auch die Summe $7\cdot 8^n + 8^n - 1$ und somit $8^{n+1}-1$ durch $7$ teilbar.

4. $n=1$: \[ n^3 - n = 1^3 - 1 = 1 - 1 = 0 \] und $0$ ist durch $3$ teilbar.

   $n \rightarrow n+1$: \begin{eqnarray*} (n+1)^3 - (n+1) & = & n^3 + 3n^2 + 3n + 1 - n - 1 \\[2mm] & = & (n^3 - n) + 3(n^2 + n) \end{eqnarray*} Der Summand $n^3 - n$ ist nach Induktionsvoraussetzung durch $3$ teilbar, der Summand $3(n^2+n)$ ist wegen der $3$ als Faktor durch $3$ teilbar.

   Also ist auch die Summe $(n^3 - n) + 3(n^2 + n)$ und somit $(n+1)^3 - (n+1)$ durch $3$ teilbar.

1. Wir führen für die rechte Summe eine Indexverschiebung durch, so dass der Summand bei beiden Summen identisch ist. \begin{eqnarray*} \sum_{k=2}^n \frac{1}{k+2} - \sum_{k=4}^{n+2} \frac{1}{k-2} & = & \sum_{k=2}^n \frac{1}{k+2} - \sum_{k=0}^{n-2} \frac{1}{k+2} \end{eqnarray*} Damit heben sich alle Summanden, die in beiden Summen auftreten, auf. Übrig bleiben in der linken Summe die Summanden für $k=n-1$ und $k=n$ und in der rechten Summe die Summanden für $k=0$ und $k=1$. Somit: \[ = \frac{1}{n+1} + \frac{1}{n+2} - \frac{1}{2} - \frac{1}{3}. \]

2. Wir teilen zunächst die Summen auf. \begin{eqnarray*} \sum_{k=2}^{n+1}\left(\frac{1}{k+2} - \frac{1}{k-1}\right) & = & \sum_{k=2}^{n+1} \frac{1}{k+2} - \sum_{k=2}^{n+1} \frac{1}{k-1} \end{eqnarray*} Jetzt führen wir in der rechten Summe eine Indexverschiebung durch, so dass die Summen identische Summanden haben. \[ = \sum_{k=2}^{n+1} \frac{1}{k+2} - \sum_{k=-1}^{n-2} \frac{1}{k+2} \] Jetzt fallen wieder alle Summanden weg, die in beiden Summen auftreten. \[ = \frac{1}{n+1} + \frac{1}{n+2} + \frac{1}{n+3} - 1 -\frac{1}{2} - \frac{1}{3}. \]

1. Wir nutzen die Definition für den Binomialkoeffizienten. \begin{eqnarray*} \binom{7}{3} & = & \frac{7\cdot 6\cdot 5}{3!} \\[2mm] & = & \frac{7\cdot 6\cdot 5}{6} \\[2mm] & = & 7\cdot 5 \\[2mm] & = & 35 \end{eqnarray*}

2. Der Binomialkoeffizient $\binom{n}{0}$ ist für $n\in\N_0$ immer $1$. Also: \[ \binom{99}{0} = 1. \]

3. Wir nutzen die Symmetrie $\binom{n}{k} = \binom{n}{n-k}$. \begin{eqnarray*} \binom{9}{7} & = & \binom{9}{2} \\[2mm] & = & \frac{9\cdot 8}{1\cdot 2} \\[2mm] & = & 9\cdot 4 \\[2mm] & = & 36 \end{eqnarray*}

4. Die Summe können wir leicht mit dem Additionstheorem $\binom{n-1}{k-1} + \binom{n-1}{k} = \binom{n}{k}$ auswerten. Damit ergibt sich: \begin{eqnarray*} \binom{8}{2} + \binom{8}{3} & = & \binom{9}{3} \\[2mm] & = & \frac{9\cdot 8 \cdot 7}{1\cdot 2 \cdot 3} \\[2mm] & = & 3\cdot 4\cdot 7 \\[2mm] & = & 84. \end{eqnarray*}

5. Wir nutzen die Definition der Fakultät. \begin{eqnarray*} 8! & = & 1\cdot 2 \cdot 3 \cdot \ldots \cdot 8 \\[2mm] & = & 6 \cdot 4 \cdot \ldots \cdot 8 \\[2mm] & = & 24 \cdot 5 \cdot \ldots \cdot 8 \\[2mm] & = & 120 \cdot 6 \cdot 7 \cdot 8 \\[2mm] & = & 720 \cdot 7 \cdot 8 \\[2mm] & = & 5040 \cdot 8 \\[2mm] & = & 40320 \end{eqnarray*}

6. Wir kürzen den Bruch: \begin{eqnarray*} \frac{20!}{18!} & = & \frac{1\cdot 2\cdot \ldots \cdot 18 \cdot 19\cdot 20}{1\cdot 2\cdot \ldots \cdot 18} \\[2mm] & = & 19\cdot 20 \\[2mm] & = & 380 \end{eqnarray*}

1. Wir nutzen den binomischen Lehrsatz: \begin{eqnarray*} \sum_{k=0}^{10} \binom{10}{k} & = & \sum_{k=0}^{10} \binom{10}{k} 1^{10-k} 1^k \\[2mm] & = & (1+1)^{10} \\[2mm] & = & 2^{10} \\[2mm] & = & 1024. \end{eqnarray*}

2. Auch hier nutzen wir wieder den binomischen Lehrsatz: \begin{eqnarray*} 1.1^4 & = & \left(1 + \frac{1}{10}\right)^4 \\[2mm] & = & \binom{4}{0}1^4\left(\frac{1}{10}\right)^0 + \binom{4}{1} 1^3 \left(\frac{1}{10}\right)^1 + \binom{4}{2} 1^2 \left(\frac{1}{10}\right)^2 + \binom{4}{3} 1^1 \left(\frac{1}{10}\right)^3 + \binom{4}{4} 1^0 \left(\frac{1}{10}\right)^4 \\[2mm] & = & 1 + \frac{4}{10} + \frac{6}{100} + \frac{4}{1000} + \frac{1}{10000} \\[2mm] & = & 1.4641. \end{eqnarray*}

3. Mit einer cleveren Umformung können wir diese Summe leicht berechnen. \begin{eqnarray*} \sum_{k=1}^8 k\cdot k! & = & \sum_{k=1}^8 ((k+1)-1)k! \\[2mm] & = & \sum_{k=1}^8 (k+1)k! - \sum_{k=1}^8 k! \\[2mm] & = & \sum_{k=1}^8 (k+1)! - \sum_{k=1}^8 k! \end{eqnarray*} Wir verschieben in der linken Summe den Index. \[ = \sum_{k=2}^9 k! - \sum_{k=1}^8 k! \] Jetzt fallen wieder fast alle Summanden weg und wir können die Summe berechnen. \begin{eqnarray*} & = & 9! - 1! \\[2mm] & = & 9\cdot 8! - 1 \end{eqnarray*} Den Wert für $8!$ kennen wir aus Übung 3 (v). \begin{eqnarray*} & = & 9\cdot 40320 - 1 \\[2mm] & = & 362880 - 1 \\[2mm] & = & 362879. \end{eqnarray*}

4. Mit der konsequenten Anwendung von einfachen Termunformungen kommen wir zum Ergebnis. Zunächst fassen wir die beiden Brüche zusammen, indem wir den Hauptnenner bilden. \[ \frac{1}{2}\left(\sqrt{3}-3\right) - \frac{1}{\sqrt{3} - 1} = \frac{(\sqrt{3}-3)(\sqrt{3}-1)-2}{2(\sqrt{3}-1)} \] Wir multiplizieren im Zähler aus \[ = \frac{3-3\sqrt{3} - \sqrt{3} + 3 - 2}{2(\sqrt{3}-1)} \] und fassen zusammen. \[ = \frac{4-4\sqrt{3}}{2(\sqrt{3}-1)} \] Wir klammern im Zähler den Faktor $4$ aus und ziehen die Brüche auseinander. \[ = \frac{4}{2}\cdot \frac{1-\sqrt{3}}{\sqrt{3} - 1} \] Jetzt kürzen wir den linken Bruch und drehen im rechten Bruch das Vorzeichen herum. \[ = 2 \left(- \frac{\sqrt{3}-1}{\sqrt{3}-1}\right) \] Damit wir der Bruch zu $1$ und es ergibt sich \[ = 2(-1) = -2. \]

1. Hier nutzen wir wieder den binomischen Lehrsatz. \begin{eqnarray*} (x+2y)^5 - (x-2y)^5 & = & \binom{5}{0}x^5(2y)^0 + \binom{5}{1}x^4(2y)^1 + \binom{5}{2}x^3(2y)^2 + \binom{5}{3}x^2(2y)^3 + \binom{5}{4}x^1(2y)^4 + \binom{5}{5}x^0(2y)^5 \\ & & - \left( \binom{5}{0}x^5(2y)^0 - \binom{5}{1}x^4(2y)^1 + \binom{5}{2}x^3(2y)^2 - \binom{5}{3}x^2(2y)^3 + \binom{5}{4}x^1(2y)^4 - \binom{5}{5}x^0(2y)^5 \right) \end{eqnarray*} Man sieht, dass sich die Terme mit $x^5, x^3, x^1$ aufheben und die anderen verdoppeln. \begin{eqnarray*} & = & 2\left(\binom{5}{1}x^4(2y)^1 + \binom{5}{3}x^2(2y)^3 + \binom{5}{5}x^0(2y)^5 \right) \\[2mm] & = & 2\left(10x^4y + 80x^2y^3 + 32 y^5\right) \\[2mm] & = & 20x^4y + 160 x^2y^3 + 64 y^5. \end{eqnarray*}

2. Termumformungen und binomische Formeln führen zum Ergebnis. \begin{eqnarray*} (a+b)^2 + (a-b)^2 + 2(a+b)(b-a) & = & (a+b)^2 + (a-b)^2 - 2(a+b)(a-b) \\[2mm] & = & (a^2 + 2ab + b^2) + (a^2 -2ab -b^2) - 2(a^2-b^2) \\[2mm] & = & 2a^2 + 2b^2 -2a^2 + 2b^2 \\[2mm] & = & 4b^2 \end{eqnarray*}

3. Natürlich verwenden wir hier wieder den binomische Lehrsatz. \begin{eqnarray*} \left( 1 - \frac{a}{3}\right)^6 & = & \binom{6}{0}1^6\left(\frac{a}{3}\right)^0 - \binom{6}{1}1^5\left(\frac{a}{3}\right)^1 + \binom{6}{2}1^4\left(\frac{a}{3}\right)^2 - \binom{6}{3}1^3\left(\frac{a}{3}\right)^3 + \binom{6}{4}1^2\left(\frac{a}{3}\right)^4 - \binom{6}{5}1^1\left(\frac{a}{3}\right)^5 + \binom{6}{6}1^0\left(\frac{a}{3}\right)^6 \\[2mm] & = & 1 - 6\frac{a}{3} + 15\frac{a^2}{9} - 20\frac{a^3}{27} + 15\frac{a^4}{81} - 6\frac{a^5}{243} + \frac{a^6}{729} \\[2mm] & = & 1 - 2a + \frac{5a^2}{3} - \frac{20a^3}{27} + \frac{5a^4}{27} - \frac{2a^5}{81} + \frac{a^6}{729} \end{eqnarray*}

1. Auch hier führt wieder eine konsequente Termumformung zum Ziel. \begin{eqnarray*} k\binom{n}{k} & = & k\cdot \frac{n!}{k!(n-k)!} \\[2mm] & = & \frac{n!}{(k-1)!(n-k)!} \\[2mm] & = & \frac{n!}{(k-1)!((n-1)-(k-1))!} \\[2mm] & = & n\cdot\frac{(n-1)!}{(k-1)!((n-1)-(k-1))!} \\[2mm] & = & n\binom{n-1}{k-1} \end{eqnarray*}

2. Wir können in der Summe die Formel aus (i) anwenden. \begin{eqnarray*} \sum_{k=1}^n \binom{n}{k}k & = & \sum_{k=1}^n n \binom{n-1}{k-1} \end{eqnarray*} Innerhalb der Summe ist $n$ eine Konstante, die wir ausklammern können. \[ = n \sum_{k=1}^n \binom{n-1}{k-1} \] Wir machen eine Indexverschiebung. \[ = n \sum_{k=0}^{n-1} \binom{n-1}{k} \] und bereiten die Anwendung des binomischen Lehrsatzes vor. \[ = n \sum_{k=0}^{n-1} \binom{n-1}{k} 1^{n-1-k} 1^k \] Damit ergibt sich \begin{eqnarray*} & = & n(1+1)^{n-1} \\[2mm] & = & n 2^{n-1}. \end{eqnarray*}

1. Die erste Gleichung können wir einfach mit der $p$-$q$-Formel lösen. \begin{eqnarray*} x^2 - x = 1 & \Rightarrow & x^2 - x - 1 = 0 \\[2mm] & \Rightarrow & x_{1,2} = \frac{1}{2} \pm \sqrt{\frac{1}{4} + 1 } \\[2mm] & \Rightarrow & x_{1,2} = \frac{1}{2} \pm \sqrt{\frac{5}{4}} \\[2mm] & \Rightarrow & x_{1,2} = \frac{1 \pm \sqrt{5}}{2} \end{eqnarray*}

2. Für diese Gleichung vierten Grades haben wir keine Formel zur Verfügung. Wir können aber versuchen, eine Lösung zu erraten. Hierzu setzen wir einfach für $x$ verschiedene Werte ein. Für $x=1$ ergibt sich: \[ 1^4 - 1^3 - 3\cdot 1^2 + 5\cdot 1 - 2 = 1 - 1 - 3 + 5 - 2 = 0. \] Damit ist $x_1 = 1$ eine erste Lösung.

   Nun wenden wir Polynomdivision an. Da $x_1=1$ eine Nullstelle des Polynoms $f(x) = x^4 - x^3 - 3x^2 + 5x - 2$ ist, muss sich dieses Polynom durch $x-1$ ohne Rest teilen lassen.

   Es ergibt sich: \[ (x^4 - x^3 - 3x^2 + 5x - 2) : (x-1) = x^3 -3x + 2. \] Die Nullstellen von $g(x) = x^3 - 3x + 2$ sind nun genau die weiteren Nullstellen von $f(x)$.

   Als Polynom dritten Grades haben wir auch für $g(x)$ keine Formel zur direkten Berechnung der Nullstellen zur Verfügung. Deshalb raten wir ein weiteres mal. Wegen \[ 1^3 - 3\cdot 1 + 2 = 0 \] erhalten wir wiederum $x_2 = 1$ als Nullstelle.

   Mit der Polynomdivision \[ (x^3 - 3x + 2) : (x-1) = x^2 + x - 2 \] erhalten wir ein Restpolynom zweiten Grades, für das wir die beiden verbleibenden Nullstellen mit der $p$-$q$-Formel berechnen können. \begin{eqnarray*} x_{3,4} & = & -\frac{1}{2} \pm \sqrt{\frac{1}{4} + 2} \\[2mm] & = & -\frac{1}{2} \pm \sqrt{\frac{9}{4}} \\[2mm] & = & -\frac{1}{2} \pm \frac{3}{2} \\[2mm] & = & 1,\quad -2. \end{eqnarray*} Wir haben damit $1$ und $-2$ als verschiedene Lösungen der Gleichung.

   Dabei ist $x_{1,2,3} = 1$ eine dreifache Nullstelle von $f(x) = x^4 - x^3 - 3x^2 + 5x - 2$ und $x_4 = -2$ eine einfache. Die Faktorisierung des Polynoms $f(x)$ lautet somit \[ x^4 - x^3 - 3x^2 + 5x - 2 = (x-1)^3(x+2). \]

3. Für diese Gleichung bietet sich eine Substitution an. Wir setzen: \[ y = x^8. \] Damit wird die ursprüngliche Gleichung zu \[ y^2 + y - 2 = 0 \] Als Lösungen erhalten wir mit der $p$-$q$-Formel \begein{eqnarray*} y_{1,2} & = & -\frac{1}{2} \pm \sqrt{\frac{1}{4} + 2} \\[2mm] & = & -\frac{1}{2} \pm \sqrt{\frac{9}{4}} \\[2mm] & = & -\frac{1}{2} \pm \frac{3}{2} \\[2mm] & = & 1,\quad -2. \end{eqnarray*} Damit können wir nun die möglichen Lösungen für $x$ bestimmen. Für \[ x^8 = 1 \] ergeben sich $1$ und $-1$ als reelle Lösungen. Für \[ x^8 = -2 \] gibt es keine reelle Lösung.

   Also sind $1$ und $-1$ alle reellen Lösungen der Gleichung.

1. Wir nutzen Potenzgesetze, um die Potenzen so umzuformen, dass sie den gleichen Exponenten haben. Es gilt \[ 4^{90} = 4^{3\cdot 30} = \left(4^3\right)^{30} = \left(2^6\right)^{30} = 64^{30} \] und \[ 3^{120} = 3^{4\cdot 30} = \left(3^4\right)^{30} = 81^{30}. \] Also: $3^{120} > 64^{30}$.

2. Neben Potenzgesetzen nutzen wir hier auch Abschätzungen. Es gilt: \begin{eqnarray*} 2^{567} & = & 2^2 \cdot 2^{565} \\[2mm] & = & 4 \cdot 2^{565} \\[2mm] & > & 2^{565} \\[2mm] & = & 2^{5\cdot 113} \\[2mm] & = & \left(2^5\right)^{113} \\[2mm] & = & 32^{113} \\[2mm] & > & 30^{113} \\[2mm] & > & 30^{100}. \end{eqnarray*}

3. Hier schätzen wir den größeren Term nach unten und den kleineren Term nach oben durch eine Zweierpotenz ab. Es gilt \[ 33^{44} > 32^{44} = \left(2^5\right)^{44} = 2^{5\cdot 44} = 2^{220} \] und \[ 44^{33} < 64^{33} = \left(2^6\right)^{33} = 2^{6\cdot 33} = 2^{198}. \] Also gilt: $44^{33} < 33^{44}$.

Alle Fragen lassen sich mithilfe der Bernoullischen Ungleichung beantworten.

1. Wir stellen $1.1^{100}$ so dar, dass wir die Bernoullischen Ungleichung nutzen können. \begin{eqnarray*} 1.1^{100} & = & \left(1 + \frac{1}{10}\right)^{100} \\[2mm] & \geq & 1 + 100\cdot \frac{1}{10} \\[2mm] & = & 1 + 10 \\[2mm] & = & 11 \end{eqnarray*}

2. Hier schätzen wir $\pi$ ab, bevor wir die Bernoullischen Ungleichung anwenden. \begin{eqnarray*} (\pi-2)^8 & > & (3.14 - 2)^8 \\[2mm] & = & 1.14^8 \\[2mm] & = & \left(1+\frac{14}{100}\right)^8 \\[2mm] & \geq & 1 + 8\cdot\frac{14}{100} \\[2mm] & = & 1 + \frac{112}{100} \\[2mm] & > & 1 + 1 \\[2mm] & = & 2 \end{eqnarray*}

3. Analog zu (i). \begin{eqnarray*} \left(\frac{3}{2}\right)^6 & = & \left(1+\frac{1}{2}\right)^6 \\[2mm] & \geq & 1 + 6\cdot\frac{1}{2} \\[2mm] & = & 1 + 3 \\[2mm] & = & 4 \end{eqnarray*}

4. Wir können die Bernoullische Ungleichung auch für negative $x \geq -1$ anwenden. Hier: $x=-0.01$. \begin{eqnarray*} 0.99^{10} & = & (1-0.01)^{10} \\[2mm] & = & \left(1 - \frac{1}{100}\right)^{10} \\[2mm] & \geq & 1 - 10\cdot \frac{1}{100} \\[2mm] & = & 1 - \frac{1}{10} \\[2mm] & = & \frac{9}{10} \\[2mm] & = & 0.9 \end{eqnarray*}

1. Wir führen den Beweis mit vollständiger Induktion.

   $n=1$: \[ \prod_{i=1}^n (1+a_i) = \prod_{i=1}^1 (1+a_i) = (1+a_1) = 1 + \sum_{i=1}^1 a_i = 1 + \sum_{i=1}^n a_i \]

   $n \rightarrow n+1$: Wir starten mit der Induktionsvoraussetzung. \[ \prod_{i=1}^n (1+a_i) \geq 1 + \sum_{i=1}^n a_i \] Wir multiplizieren die Ungleichung mit $1 + a_{n+1}$. Wegen $a_{n+1} \geq 0$ ist dieser Faktor positiv und $\geq$ bleibt erhalten. \[ \Rightarrow\quad (1+a_{n+1}) \prod_{i=1}^n (1+a_i) \geq (1+a_{n+1}) \left(1 + \sum_{i=1}^n a_i\right) \] Auf der linken Seite nehmen wir $1+a_{n+1}$ im Produkt auf und auf der rechten Seite multiplizieren wir aus. \[ \Rightarrow\quad \prod_{i=1}^{n+1} (1+a_i) \geq 1 + a_{n+1} + \sum_{i=1}^n a_i + a_{n+1}\sum_{i=1}^n a_i \] Wir nehmen $a_{n+1}$ in die Summe auf. \[ \Rightarrow\quad \prod_{i=1}^{n+1} (1+a_i) \geq 1 + \sum_{i=1}^{n+1} a_i + a_{n+1}\sum_{i=1}^n a_i \] Mit $a_{n+1}\sum_{i=1}^n a_i \geq 0$ folgt: \[ \Rightarrow\quad \prod_{i=1}^{n+1} (1+a_i) \geq 1 + \sum_{i=1}^{n+1} a_i. \]

2. Mit \[ a := a_1 = a_2 = \cdots = a_n \] entsteht die Ungleichung \[ (1+a)^n \geq 1 + na. \] Dies ist die Bernoullische Ungleichung.

   Wir haben also in (i) eine Verallgemeinerung der Bernoullischen Ungleichung bewiesen.

1. Wir lösen nach $x$ auf. \begin{eqnarray*} 17a + bx = 2x + 3 & \Leftrightarrow & bx - 2x = 3 - 17a \\[2mm] & \Leftrightarrow & (b-2)x = 3 - 17a \\[2mm] & \Leftrightarrow & x = \frac{3-17a}{b-2} \end{eqnarray*} wenn $b\neq 2$ gilt.

   Fall 1: $b \neq 2$: Dann ist \[ x = \frac{3-17a}{b-2} \] die eindeutige Lösung.

   Für $b=2$ wird die Gleichung zu \[ 17a + 2x = 2x + 3 \quad \Leftrightarrow \quad 17a = 3. \] Damit können wir zwei weitere Fälle unterscheiden.

   Fall 2: $b=2 \wedge a=\frac{3}{17}$: Dann erfüllen alle $x\in\R$ die Gleichung.

   Fall 3: $b=2 \wedge a\neq\frac{3}{17}$: Dann existiert keine Lösung.

2. Wir multiplizieren die Gleichung mit $ax-c$ und $a-b$. \begin{eqnarray*} \frac{ax+c}{ax-c} = \frac{a+b}{a-b} & \Leftrightarrow & (a-b)(ax+c) = (a+b)(ax-c) \\[2mm] & \Leftrightarrow & a^2x - abx + ac - bc = a^2x + abx - ac - bc \\[2mm] & \Leftrightarrow & -abx + ac = abx - ac \\[2mm] & \Leftrightarrow & 2abx = 2ac \\[2mm] & \Leftrightarrow & abx = ac \\[2mm] & \Leftrightarrow & abx - ac = 0 \\[2mm] & \Leftrightarrow & a(bx-c) = 0 \end{eqnarray*} Diese Gleichung ist für $a=0$ oder $bx-c=0$ erfüllt.

   Fall 1: $a=0$: Dann wird die Gleichung zu $-1 = -1$ und ist damit für alle $x\in\R$ erfüllt.

   Fall 2: $a\neq 0 \wedge b\neq 0$: Dann ist $x = \frac{c}{b}$ die eindeutige Lösung.

   Fall 3: $a\neq 0 \wedge b= 0 \wedge c=0$: Dann ist die Gleichung für alle $x\in\R$ erfüllt.

   Fall 4: $a\neq 0 \wedge b= 0 \wedge c\neq 0$: Dann existiert keine Lösung.

1. Wir lösen die Ungleichung nach $x$ auf. \begin{eqnarray*} x + 2 \geq 4 - x & \Leftrightarrow & 2x \geq 2 \\[2mm] & \Leftrightarrow & x \geq 1 \end{eqnarray*} Damit ergibt sich als Lösungsmenge: \[ {\cal L}_1 = \{x\in\R| x\geq 1\}. \]

2. Wir lösen die Ungleichung nach $x$ auf. \begin{eqnarray*} 3-2x \leq x - 9 & \Leftrightarrow& 12 \leq 3x \\[2mm] & \Leftrightarrow & 3x \geq 12 \\[2mm] & \Leftrightarrow & x \geq 4 \end{eqnarray*} Damit ergibt sich als Lösungsmenge: \[ {\cal L}_2 = \{x\in\R| x\geq 4\}. \]

3. Wir lösen die Ungleichung nach $x$ auf. \begin{eqnarray*} 13x - 2 < 16x - 5 & \Leftrightarrow & 3 < 3x \\[2mm] & \Leftrightarrow & x > 1 \end{eqnarray*} Damit ergibt sich als Lösungsmenge: \[ {\cal L}_3 = \{x\in\R| x > 1\}. \]

4. Wir lösen die Ungleichung nach $x$ auf. \begin{eqnarray*} \frac{x}{3} + 1 < 3 - \frac{3}{2}x & \Leftrightarrow & \frac{3}{2}x + \frac{x}{3} < 2 \\[2mm] & \Leftrightarrow & \left(\frac{3}{2}+\frac{1}{3}\right)x < 2 \\[2mm] & \Leftrightarrow & \frac{11}{6}x < 2 \\[2mm] & \Leftrightarrow & x < \frac{12}{11} \end{eqnarray*} Damit ergibt sich als Lösungsmenge: \[ {\cal L}_4 = \left\{x\in\R| x < \frac{12}{11}\right\}. \]

1. Wenn wir die Ungleichung mit dem Nenner $3-2x$ multiplizieren, müssen wir eine Fallunterscheidung machen, denn nur für $3-2x > 0$ bleibt $\geq$ in der Ungleichung erhalten, ansonsten wird aus $\geq$ ein $\leq$.

   Es gilt $3-2x > 0 \Leftrightarrow x < \frac{3}{2}$.

   Fall (a): $x < \frac{3}{2}$: \begin{eqnarray*} \frac{3x+2}{3-2x} \geq 2 & \Leftrightarrow & 3x + 2 \geq 2(3-2x) \\[2mm] & \Leftrightarrow & 3x + 2 \geq 6 - 4x \\[2mm] & \Leftrightarrow & 7x \geq 4 \\[2mm] & \Leftrightarrow & x \geq \frac{4}{7} \end{eqnarray*} Damit haben wir als Lösungsmenge für diesen Fall \[ {\cal L}_{1,a} = \left\{x\in\R | \frac{4}{7} \leq x < \frac{3}{2}\right\}. \]

   Fall (b): $x > \frac{3}{2}$: \begin{eqnarray*} \frac{3x+2}{3-2x} \geq 2 & \Leftrightarrow & 3x + 2 \leq 2(3-2x) \\[2mm] & \Leftrightarrow & x \leq \frac{4}{7} \end{eqnarray*} Jetzt steht aber $x \leq \frac{4}{7}$ im Widerspruch zu $x > \frac{3}{2}$. Deshalb: \[ {\cal L}_{1,b} = \emptyset. \]

   Damit ergibt sich als Gesamtlösungsmenge \[ {\cal L}_1 = \left\{x\in\R | \frac{4}{7} \leq x < \frac{3}{2}\right\}. \]

2. Auch hier müssen wir eine Fallunterscheidung durchführen.

   Fall (a): $x > -2$: \begin{eqnarray*} \frac{3x+5}{x+2} < 4 & \Leftrightarrow & 3x+5 < 4(x+2) \\[2mm] & \Leftrightarrow & 3x + 5 < 4x + 8 \\[2mm] & \Leftrightarrow & -3 < x \end{eqnarray*} Wir müssen aber berücksichtigen, dass dieser Fall nur für $x > -2$ gültig ist. Daher ergibt sich als Lösungsmenge für diesen Fall \[ {\cal L}_{2,a} = \{x\in\R|x > -2\}. \]

   Fall (a): $x < -2$: \begin{eqnarray*} \frac{3x+5}{x+2} < 4 & \Leftrightarrow & 3x+5 > 4(x+2) \\[2mm] & \Leftrightarrow & -3 > x \end{eqnarray*} Also: \[ {\cal L}_{2,b} = \{x\in\R|x < -3\}. \]

   Damit ergibt sich als Gesamtlösungsmenge \[ {\cal L}_2 = {\cal L}_{2,a} \cup {\cal L}_{2,b} = \{x\in\R| x < -3 \vee x > -2 \}. \]

3. Wieder machen wir eine Fallunterscheidung.

   Fall (a): $x > -2$ \begin{eqnarray*} \frac{x-2}{4+2x} < x & \Leftrightarrow & x-2 < x(4+2x) \\[2mm] & \Leftrightarrow & x - 2 < 4x + 2x^2 \\[2mm] & \Leftrightarrow & 2x^2 + 3x + 2 > 0 \\[2mm] & \Leftrightarrow & x^2 + \frac{3}{2}x+1 > 0 \\[2mm] & \Leftrightarrow & \left(x+\frac{3}{4}\right)^2 -\frac{9}{16} + 1 > 0 \\[2mm] & \Leftrightarrow & \left(x+\frac{3}{4}\right)^2 +\frac{7}{16} > 0 \end{eqnarray*} Die letzte Ungleichung ist für alle $x\in\R$ erfüllt. Damit erhalten wir \[ {\cal L}_{3,a} = \{x\in\R | x > -2\} \] als Lösungsmenge für diesen Fall.

   Fall (b): $x < -2$ \begin{eqnarray*} \frac{x-2}{4+2x} < x & \Leftrightarrow & x-2 > x(4+2x) \\[2mm] & \Leftrightarrow & \left(x+\frac{3}{4}\right)^2 +\frac{7}{16} < 0 \end{eqnarray*} Diese Ungleichung ist nicht erfüllbar. Somit \[ {\cal L}_{3,b} = \emptyset. \]

   Damit haben wir als Gesamtlösungsmenge \[ {\cal L}_3 = \{x\in\R | x > -2\}. \]

4. Wir untersuchen zuerst den Nenner. \begin{eqnarray*} x^2 + x + 6 & = & \left(x+\frac{1}{2}\right)^2 -\frac{1}{4} + 6 \\[2mm] & = & \left(x+\frac{1}{2}\right)^2 + \frac{23}{4} \\[2mm] & > & 0 \end{eqnarray*} Damit benötigen wir keine Fallunterscheidung, denn der Nenner kann niemals negativ werden. \begin{eqnarray*} \frac{x^2 + 6x + 4}{x^2 + x + 6} \geq 1 & \Leftrightarrow & x^2 + 6x + 4 \geq x^2 + x + 6 \\[2mm] & \Leftrightarrow & 6x + 4 \geq x + 6 \\[2mm] & \Leftrightarrow & 5x\geq 2 \\[2mm] & \Leftrightarrow & x \geq \frac{2}{5}. \end{eqnarray*} Also: \[ {\cal L}_4 = \left\{x\in\R| x \geq \frac{2}{5}\right\}. \]

5. Es gilt: \begin{eqnarray*} x^2 + 3x + 3 & = & \left(x+\frac{3}{2}\right)^2 -\frac{9}{4} + 3 \\[2mm] & = & \left(x+\frac{3}{2}\right)^2 + \frac{3}{4} \\[2mm] & > & 0. \end{eqnarray*} Also kann die Ungleichung nicht erfüllt werden: \[ {\cal L}_5 = \emptyset. \]

1. 

   Wir sehen, dass es anscheinend zwei Lösungen gibt, die wir nun berechnen. \begin{eqnarray*} |x+3| = 4 & \Leftrightarrow & x+3=4 \vee x+3=-4 \\[2mm] & \Leftrightarrow & x=1 \vee x=-7 \end{eqnarray*}

   Damit sind $x=1$ und $x=-7$ die beiden Lösungen der Gleichung.

2. 

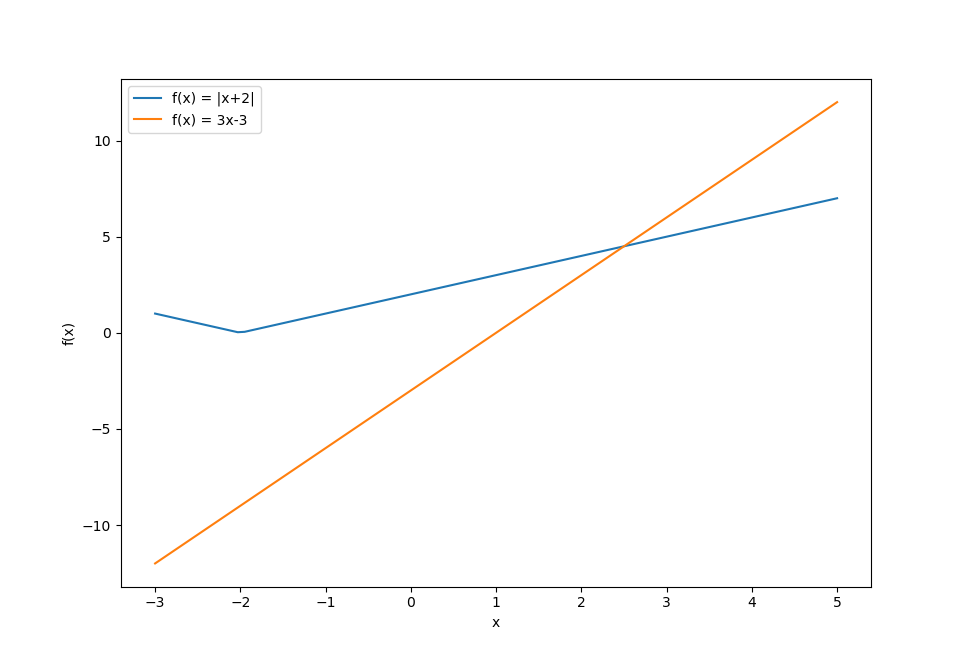
   Hier scheint es nur eine Lösung zu geben. Um dies formal korrekt nachzuweisen, müssen wir eine Fallunterscheidung durchführen, denn $x$ tritt in dieser Betragsgleichung auch außerhalb des Betrags auf.

   Es gilt \[ x+2 \geq 0 \Leftrightarrow x \geq -2. \] Dementsprechend unterscheiden wir zwischen $x\geq -2$ und $x < -2$.

   Fall (a): $x \geq -2$: \begin{eqnarray*} |x+2| = 3x-3 & \Leftrightarrow & x+2 = 3x-3 \\[2mm] & \Leftrightarrow & 5 = 2x \\[2mm] & \Leftrightarrow & x = \frac{5}{2} \end{eqnarray*} und es gilt $\frac{5}{2} \geq -2$. Fall (a) deckt also die Lösung $x = \frac{5}{2}$ ab.

   Fall (b): $x < -2$: \begin{eqnarray*} |x+2| = 3x-3 & \Leftrightarrow & -(x+2) = 3x - 3 \\[2mm] & \Leftrightarrow & -x-2 = 3x-3 \\[2mm] & \Leftrightarrow & 1 = 4x \\[2mm] & \Leftrightarrow & x = \frac{1}{4} \end{eqnarray*} Fall (b) deckt diese Lösung aber nicht ab, denn $\frac{1}{4} \not<-2$. Daher liegt hier tatsächlich keine Lösung vor.

   Also ist $x=\frac{5}{2}$ die einzige Lösung der Betragsgleichung.

3. 

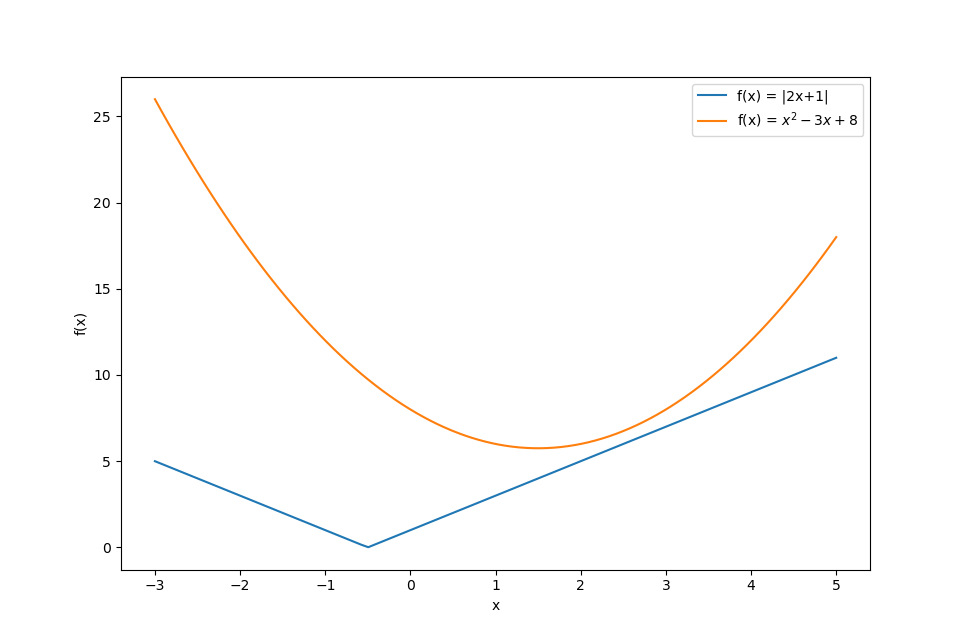
   Hier scheint es keine Lösung zu geben. Um dies zu beweisen, führen wir wieder eine Fallunterscheidung durch. Es gilt \[ 2x + 1 \geq 0 \Leftrightarrow x \geq -\frac{1}{2}. \] Dementsprechend unterscheiden wir zwischen $x \geq -\frac{1}{2}$ und $x < -\frac{1}{2}$.

   Fall (a): $x \geq -\frac{1}{2}$: \begin{eqnarray*} x^2 -3x + 8 = |2x+1| & \Leftrightarrow & x^2 -3x + 8 = 2x + 1 \\[2mm] & \Leftrightarrow & x^2 - 5x + 7 = 0 \\[2mm] & \Leftrightarrow & \left(x-\frac{5}{2}\right)^2 -\frac{25}{4} + 7 = 0 \\[2mm] & \Leftrightarrow & \left(x-\frac{5}{2}\right)^2 + \frac{3}{4} = 0 \\[2mm] & \Leftrightarrow & \left(x-\frac{5}{2}\right)^2 = -\frac{3}{4} \end{eqnarray*} Diese Gleichung ist nicht lösbar. Somit ergibt sich für diesen Fall keine Lösung.

   Fall (b): $x < -\frac{1}{2}$: \begin{eqnarray*} x^2 -3x + 8 = |2x+1| & \Leftrightarrow & x^2 -3x + 8 = -(2x+1) \\[2mm] & \Leftrightarrow & x^2 -3x + 8 = -2x -1 \\[2mm] & \Leftrightarrow & x^2 -x + 9 = 0 \\[2mm] & \Leftrightarrow & \left(x-\frac{1}{2}\right)^2 - \frac{1}{4} + 9 = 0 \\[2mm] & \Leftrightarrow & \left(x-\frac{1}{2}\right)^2 + \frac{35}{4} = 0 \\[2mm] & \Leftrightarrow & \left(x-\frac{1}{2}\right)^2 = -\frac{35}{4} \end{eqnarray*} Auch diese Gleichung ist nicht lösbar.

   Damit gibt es auch insgesamt keine Lösung für die Gleichung.

1. Es ist eine Äquivalenzaussage, daher müssen wir beide Richtungen zeigen.

   "$\Rightarrow$": Es gilt also $|x|\leq a$. Wir machen eine Fallunterscheidung.

   1. Fall: $x \geq 0$. Dann gilt $|x| = x$ und somit: \[ |x| \leq a \Rightarrow x \leq a. \] Wegen $x \geq 0$ gilt somit aber auch $a \geq 0$ bzw. $-a \leq 0$. Damit folgt \[ -a \leq x \leq a. \]

   2. Fall: $x < 0$. Dann gilt $|x| = -x$ und somit: \[ |x| \leq a \Rightarrow -x \leq a \Rightarrow x \geq -a \Rightarrow a \geq x \geq -a. \] Die letzte Folgerung gilt analog zum 1. Fall wegen $a > 0$.

   Damit ist die Richtung "$\Rightarrow$" bewiesen.

   "$\Leftarrow$": Diese Richtung lässt sich etwas einfacher zeigen. \begin{eqnarray*} -a \leq x \leq a & \Rightarrow & -a \leq x \wedge x \leq a \\[2mm] & \Rightarrow & a \geq -x \wedge a \geq x \\[2mm] & \Rightarrow & a \geq |x|, \end{eqnarray*} denn es gilt entweder $|x|=x$ oder $|x| = -x$.

2. Die Ungleichung $|x| > a$ ist die Negation der Ungleichung aus (i). Deshalb können wir den Beweis für (ii) einfach mit logischen Umformungen führen. \begin{eqnarray*} |x| > a & \Leftrightarrow & \neg(|x|\leq a) \\[2mm] & \Leftrightarrow & \neg(-a \leq x \wedge x \leq a) \\[2mm] & \Leftrightarrow & \neg(-a\leq x) \vee \neg(x\leq a) \\[2mm] & \Leftrightarrow & -a > x \vee x > a \\[2mm] & \Leftrightarrow & x < -a \vee x > a \end{eqnarray*}

1. Wir nutzen die Rechenregel (i) aus der vorigen Übung. \begin{eqnarray*} \left| \frac{3}{2}x - 2\right| \leq \frac{5}{2} & \Leftrightarrow & \frac{3}{2}x - 2 \geq -\frac{5}{2} \wedge \frac{3}{2}x - 2 \leq \frac{5}{2} \\[2mm] & \Leftrightarrow & \frac{3}{2}x \geq -\frac{1}{2} \wedge \frac{3}{2}x \leq \frac{9}{2} \\[2mm] & \Leftrightarrow & x \geq -\frac{1}{3} \wedge x \leq 3 \end{eqnarray*} Damit ist \[ {\cal L}_1 = \left\{x\in\R | -\frac{1}{3} \leq x \leq 3 \right\} \] die Lösungsmenge dieser Betragsungleichung.

2. Wir nutzen die Rechenregel (ii) aus der vorigen Übung, die auch in nicht strikter Form gilt. \begin{eqnarray*} |7x-3| \geq 5 & \Leftrightarrow & 7x-3 \leq -5 \vee 7x-3 \geq 5 \\[2mm] & \Leftrightarrow & 7x \leq -2 \vee 7x \geq 8 \\[2mm] & \Leftrightarrow & x \leq -\frac{2}{7} \vee x \geq \frac{8}{7} \end{eqnarray*} Damit lautet die Lösungsmenge \[ {\cal L}_2 = \left\{x\in\R| x \leq -\frac{2}{7}\right\} \cup \left\{x\in\R| x \geq \frac{8}{7} \right\}. \]

3. Für diese Ungleichung bietet sich eine Fallunterscheidung in drei Fälle an.

   Fall (a): $x\geq 1$: Dann gilt sowohl $x-1 \geq 0$ als auch $x+5\geq 0$. \begin{eqnarray*} |x-1| + |x+5| \leq 4 & \Leftrightarrow & (x-1) + (x+5) \leq 4 \\[2mm] & \Leftrightarrow & 2x+4 \leq 4 \\[2mm] & \Leftrightarrow & 2x \leq 0 \\[2mm] & \Leftrightarrow & x \leq 0 \end{eqnarray*} Diese Lösung steht im Widerspruch zu der Fallbedingung $x\geq 1$. Daher gibt es in diesem Fall keine Lösung.

   Fall (b): $-5 \leq x < 1$: Dann gilt $x-1<0$ und $x+5 \geq 0$. \begin{eqnarray*} |x-1| + |x+5| \leq 4 & \Leftrightarrow & -(x-1) + (x+5) \leq 4 \\[2mm] & \Leftrightarrow & 6 \leq 4 \end{eqnarray*} Die letzte Ungleichung ust stets falsch. Daher gibt es auch in diesem Fall keine Lösung.

   Fall (c): $x < -5$: Dann gilt $x-1<0$ und $x+5 < 0$. \begin{eqnarray*} |x-1| + |x+5| \leq 4 & \Leftrightarrow & -(x-1) - (x+5) \leq 4 \\[2mm] & \Leftrightarrow & -2x-4 \leq 4 \\[2mm] & \Leftrightarrow & -2x \leq 8 \\[2mm] & \Leftrightarrow & x \geq -4 \end{eqnarray*} Diese Lösung steht im Widerspruch zu der Fallbedingung $x < 5$. Daher gibt es auch in diesem Fall keine Lösung.

   Die Ungleichung ist somit unlösbar: \[ {\cal L}_3 = \emptyset. \]

4. Es bietet sich an, vor einer Fallunterscheidung die Ungleichung zu vereinfachen. \begin{eqnarray*} \left|\frac{x-3}{2x+4}\right| < 1 & \Leftrightarrow & \frac{|x-3|}{|2x+4|} < 1 \\[2mm] & \Leftrightarrow & |x-3| < |2x+4| \end{eqnarray*} Für diese Ungleichung bietet sich wiederum eine Unterscheidung in drei Fälle an.

   Fall (a): $x\geq 3$: Dann gilt $x-3 \geq 0$ und $2x+4 \geq 0$ und somit \begin{eqnarray*} |x-3| < |2x+4| & \Leftrightarrow & x-3 < 2x + 4 \\[2mm] & \leftrightarrow & 0 < x + 7 \\[2mm] & \Leftrightarrow & x > -7 \end{eqnarray*} Damit ist \[ {\cal L}_{4,a} = \{x\in\R| x\geq 3\} \] die Lösungsmenge für diesen Fall.

   Fall (b): $-2 \leq x < 3$: Dann gilt $x-3 < 0$ und $2x+4 \geq 0$ und somit \begin{eqnarray*} |x-3| < |2x+4| & \Leftrightarrow & -(x-3) < 2x + 4 \\[2mm] & \Leftrightarrow & -x+3 < 2x + 4 \\[2mm] & \Leftrightarrow & -1 < 3x \\[2mm] & \leftrightarrow & x > -\frac{1}{3} \end{eqnarray*} Damit ist \[ {\cal L}_{4,b} = \{x\in\R| -\frac{1}{3} < x < 3\} \] die Lösungsmenge für diesen Fall.

   Fall (c): $x < -2: Dann gilt $x-3 < 0$ und $2x+4 < 0$ und somit \begin{eqnarray*} |x-3| < |2x+4| & \Leftrightarrow & -(x-3) < -(2x+4) \\[2mm] & \Leftrightarrow & -x+3 < -2x -4 \\[2mm] & \Leftrightarrow & x < -7 \end{eqnarray*} Damit ist \[ {\cal L}_{4,c} = \{x\in\R| x < -7\} \] die Lösungsmenge für diesen Fall.

   Insgesamt ergibt sich somit \[ {\cal L}_4 = \left\{ x\in\R| x < -7 \vee x > -\frac{1}{3} \right\} \] als Lösungsmenge.

5. Auch hier kannst Du Fallunterscheidungen nutzen, um die Lösungsmenge zu bestimmen. Dann kommt heraus, dass die Ungleichung für alle $x\in\R$ gilt. Dies kannst Du aber auch viel einfacher zeigen.

   Für den einfachen Nachweis nutzen wir die umgekehrte Dreiecksungleichung in der Form \[ ||a|-|b|| \leq |a-b|. \] Diese wenden wir auf die hier gegebene Ungleichung mit $a=x+1$ und $b=x+3$ an. Dann ergibt sich \[ ||x+1| - |x+3|| \leq |(x+1) - (x+3)| = |-2| = 2 < 3. \] Also ist die Ungleichung für alle $x\in\R$ erfüllt.

Zuerst multiplizieren wir die zweite und dritte Ungleichung mit $-1$, so dass wir ausschließlich $\leq$-Ungleichungen haben. \begin{eqnarray*} 3x + y & \leq & 15 \\ -x + 2y & \leq & -4 \\ -7x - 7y & \leq & -37 \end{eqnarray*} Wir entscheiden uns, die Variable $x$ zu eliminieren. Hierzu multiplizieren wir die Ungleichungen mit verschiedenen Faktoren, so dass die Koeffizienten vor $x$ alle den gleichen Betrag haben. Deshalb multiplizieren wir die erste Gleichung mit $7$, die zweite mit $21$ und die dritte mit $3$. \begin{eqnarray*} 21x + 7y & \leq & 105 \\ -21x + 42y & \leq & -84 \\ -21x - 21y & \leq & -111 \end{eqnarray*} Jetzt addieren wir die erste und zweite Ungleichung sowie die erste und dritte Ungleichung. Wir erhalten: \begin{eqnarray*} 49y \leq 21 \\ -14y \leq -6 \end{eqnarray*} Aus der ersten Unlgeichung folgt \[ y\leq \frac{21}{49} = \frac{3}{7} \] und aus der zweiten Ungleichung folgt \[ y \geq \frac{-6}{-14} = \frac{3}{7}. \] Also muss \[ y = \frac{3}{7} \] gelten.

Wir setzen nun diesen Wert für $y$ in das originäre Ungleichungssystem ein. Für die erste Ungleichung erhalten wir: \begin{eqnarray*} 3x + y \leq 15 & \Rightarrow & 3x + \frac{3}{7} \leq 15 \\[2mm] & \Rightarrow & 3x \leq 15 - \frac{3}{7} = \frac{105-3}{7} = \frac{102}{7} \\[2mm] & \Rightarrow & x \leq \frac{102}{21} = \frac{34}{7}. \end{eqnarray*} Mit der zweiten Gleichung ergibt sich: \begin{eqnarray*} x-2y \geq 4 & \Rightarrow & x - \frac{6}{7} \geq 4 \\[2mm] & \Rightarrow & x \geq 4 + \frac{6}{7} = \frac{28+6}{7} = \frac{34}{7}. \end{eqnarray*} Damit muss $x=\frac{34}{7}$ gelten.

Wir müssen aber noch prüfen, ob damit auch die dritte Ungleichung erfüllt ist: \begin{eqnarray*} 7x+7y & = & 7\cdot\frac{34}{7} + 7\cdot\frac{3}{7} \\[2mm] & = & 34 + 3 \\[2mm] & = & 37 \leq 37. \end{eqnarray*} Also ist die Ungleichung erfüllt.

Damit ist \[ x= \frac{34}{7},\quad y=\frac{3}{7} \] die eindeutige Lösung des Ungleichungssystems.

1. $n=3$: Es gilt \[ 2^n = 2^3 = 8 > 6 = 2\cdot 3 = 2n. \]

   $n \rightarrow n+1$: Es gilt \[ 2^{n+1} = 2\cdot 2^n > 2\cdot 2n = 2n+2n > 2n+2 = 2(n+1). \] Dabei haben wir beim ersten $>$ die Induktionsvoraussetzung genutzt.

2. $n=4$: Es gilt \[ n! = 4! = 24 > 16 = 2^4 = 2^n. \]

   $n \rightarrow n+1$: Es gilt: \[ (n+1)! = (n+1)\cdot n! > (n+1)2^n > (1+1)2^n = 2\cdot 2^n = 2^{n+1}. \] Dabei haben wir wiederum beim ersten $>$ die Induktionsvoraussetzung genutzt.

3. $n=2$: Es gilt \[ \sum_{k=0}^n \frac{1}{k!} = \sum_{k=0}^2 \frac{1}{k!} = 1 + 1 + \frac{1}{2} = \frac{5}{2} \leq \frac{5}{2} = 3 - \frac{1}{2} = 3 - \frac{1}{2^{2-1}} = 3 - \frac{1}{2^{n-1}}. \]

   $n\rightarrow n+1$: Es gilt \begin{eqnarray*} \sum_{k=0}^{n+1} \frac{1}{k!} & = & \frac{1}{(n+1)!} + \sum_{k=0}^n \frac{1}{k!} \\[2mm] & \leq & \frac{1}{(n+1)!} + 3 - \frac{1}{2^{n-1}} \end{eqnarray*} Nun nutzen wir aus, dass für alle $n\in\N$ die Ungleichung \[ (n+1)! \geq 2^n \quad(*) \] gilt. Eine ähnliche Ungleichung hatten wir in (ii) bereits gezeigt. Auch diese Ungleichung kannst Du leicht mit vollständiger Induktion beweisen.

   Mit Anwendung der Ungleichung (*) folgt: \begin{eqnarray*} & \leq & 3 - \frac{1}{2^{n-1}} + \frac{1}{2^n} \\[2mm] & = & 3 - \left(\frac{1}{2^{n-1}} - \frac{1}{2^n}\right) \\[2mm] & = & 3 - \frac{2-1}{2^n} \\[2mm] & = & 3 - \frac{1}{2^n}. \end{eqnarray*} Somit ist die Ungleichung bewiesen.