In dieser Blog-Folge zeige ich Dir ein weiteres Konvergenzkriterium für Reihen: das Integralkriterium. Mit ihm kannst Du die Frage, ob eine Reihe konvergiert, mithilfe eines uneigentlichen Integrals entscheiden.
Integralkriterium für Reihen
Bei der Betrachtung von Reihen in Kapitel 3 haben wir gelernt, dass die harmonische Reihe \[ \sum_{n=1}^\infty \frac{1}{n} \] divergent, aber die Reihe \[ \sum_{n=1}^\infty \frac{1}{n^2} \] konvergent ist. In der vorigen Blog-Folge haben wir gesehen, dass dies analog für die uneigentlichen Integrale \[ \int_1^\infty \frac{1}{x}\,dx \quad\text{und}\quad \int_1^\infty \frac{1}{x^2}\,dx \] gilt. Während das linke uneigentliche Integral divergent ist, konvergiert das rechte uneigentliche Integral.
Diese Analogie ist nicht zufällig. Vielmehr gilt unter bestimmten Voraussetzungen eine Äquivalenz bei der Konvergenz von Reihen und uneigentlichen Integralen über die selbe Funktion. Diese Äquivalenz manifestiert sich in dem Intgralkriterium für Reihen, das im nachfolgenden Satz formuliert wird.
Satz
Es sei $f:[1,\infty)\rightarrow\R$ eine monoton fallende und nicht negative Regelfunktion.
Dann gilt:
-
$\displaystyle\sum_{n=1}^\infty f(n)$ konvergiert genau dann, wenn $\displaystyle\int_1^\infty f(x)\,dx$ konvergiert.
-
Die Folge $(a_n)$ mit \[ a_n = \sum_{k=1}^n f(k) - \int_1^{n+1} f(x)\,dx \] ist konvergent.
Die Frage, ob eine eine Reihe konvergiert oder nicht, können wir mit Teil (i) des Integralkriteriums beantworten. Teil (ii) dient in erster Linie für den Beweis des Kriteriums, denn wie wir noch sehen werden, folgt (i) aus (ii).
Bevor wir uns aber dem Beweis zuwenden, schauen wir uns zunächst an, wie wir das Integralkriterium praktisch nutzen können.
Anwendungsbeispiele für das Integralkriterium
Wir starten mit einem recht einfachen Beispiel. Dabei zeige ich nicht nur die Anwendung des Integralkriteriums, sondern auch, dass wir mit Quotienten- und Wurzelkriterium die Frage nach der Konergenz nicht beantworten können.
Beispiel 1
Wir wollen entscheiden, ob die Reihe \[ \sum_{n=1}^\infty \frac{1}{n\sqrt{n}} \] konvergent ist oder nicht.
Quotienten- oder Wurzelkriterium sind hier nicht hilfreich. Mit dem Quotientenkriterium erhalten wir beispielsweise \begin{eqnarray*} \left| \frac{a_{n+1}}{a_n}\right| & = & \left| \frac{ \frac{1}{(n+1)\sqrt{n+1}} }{ \frac{1}{n\sqrt{n}} } \right| \\[2mm] & = & \frac{n\sqrt{n}}{(n+1)\sqrt{n+1}} \\[2mm] & = & \frac{n}{n+1} \sqrt{\frac{n}{n+1}} \\[2mm] & = & \frac{1}{1+\frac{1}{n}} \sqrt{\frac{1}{1+\frac{1}{n}}} \end{eqnarray*} Wegen \[ \lim_{n\rightarrow\infty} \frac{1}{1+\frac{1}{n}} = 1 \] und der Stetigkeit des Wurzelfunktion folgt somit \[ \lim_{n\rightarrow\infty} \left| \frac{a_{n+1}}{a_n}\right| = 1. \] Also ist mit dem Quotientenkriterium keine Aussage zur Konvergenz der Reihe möglich.
Bei Anwendung des Wurzelkriteriums würden wir \[ \lim_{n\rightarrow\infty} \sqrt[n]{|a_n|} = 1 \] erhalten, womit ebenfalls keine Aussage zur Konvergenz der Reihe möglich ist.
Mit dem Integralkriterium können wir aber recht leicht nachweisen, dass die Reihe konvergent ist. Zunächst müssen wir die Voraussetzungen überprüfen. Natürlich gilt \[ f(n) := \frac{1}{n\sqrt{n}} > 0 \] womit die Funktion $f(n)$ nicht negativ ist. Da $n\sqrt{n}$ monoton wachsend ist, ist $f(n)$ auch eine monoton fallende Funktion.
Mit Punkt (i) des Integralkriteriums folgt, dass die gegebene Reihe genau dann konvergiert, wenn das uneigentliche Integral \[ \int_1^\infty \frac{1}{x\sqrt{x}}\,dx \] konvergent ist. Um dies nachzuweisen, rechnen wir den Wert des uneigentlichen Integrals einfach aus.
Dafür benötigen wir eine Stammfunktion. Es gilt \[ \int \frac{1}{x\sqrt{x}}\,dx = \int x^{-\frac{3}{2}}\,dx = -2x^{-\frac{1}{2}} = - \frac{2}{\sqrt{x}} + c. \] Damit erhalten wir \begin{eqnarray*} \int_1^\infty \frac{1}{x\sqrt{x}}\,dx & = & \lim_{\beta\rightarrow\infty} \int_1^\beta \frac{1}{x\sqrt{x}}\,dx \\[2mm] & = & \lim_{\beta\rightarrow\infty} \left. -\frac{2}{\sqrt{x}} \right|_{x=1}^{x=\beta} \\[2mm] & = & \lim_{\beta\rightarrow\infty} -\frac{2}{\sqrt{\beta}} + 2 \\[2mm] & = & 2. \end{eqnarray*}
Also ist das uneigentliche Integral \[ \int_1^\infty \frac{1}{x\sqrt{x}}\,dx \] und damit auch die Reihe \[ \sum_{n=1}^\infty \frac{1}{n\sqrt{n}} \] konvergent.
Die Funktion \[ \zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s} \] heißt Riemannsche Zetafunktion. Sie spielt in der Mathematik insbesondere in der Zahlentheorie eine bedeutende Rolle.
Für $s=1$ ist die Riemannsche Zetafunktion offensichtlich nicht definiert, denn die definierende Reihe ist dann die harmonische Reihe, die aber ja divergent ist. In Beispiel 1 haben wir gezeigt, dass $\zeta(s)$ für $s=\frac{3}{2}$ definiert ist. Mit dem Majorantenkriterium folgt dann leicht, dass $\zeta(s)$ auch für alle $s > \frac{3}{2}$ definiert ist.
Wie sieht es also zwischen $1$ und $\frac{3}{2}$ aus. Wo ist die Riemannsche Zetafunktion dort definiert? Mit dem Integralkriterium können wir diese Frage leicht beantworten.
Proposition
Die Reihe \[ \sum_{n=1}^\infty \frac{1}{n^s} \] ist für alle $s > 1$ konvergent.Beweis
Im Prinzip müssen wir nur den Beweis der Konvergenz aus Beispiel 1 auf $s > 1$ verallgemeinern.
Es sei also $s > 1$. Die Funktion \[ f(n) := \frac{1}{n^s} \] ist dann nicht negativ und monoton fallend.
Für die Stammfunktion gilt: \[ \int \frac{1}{x^s}\,dx = \int x^{-s}\,dx = \frac{1}{-s+1}x^{-s+1} = \frac{1}{1-s} x^{1-s} + c. \]
Damit ergibt sich \begin{eqnarray*} \int_1^\infty \frac{1}{x^s}\,dx & = & \lim_{\beta\rightarrow\infty} \int_1^\beta \frac{1}{x^s}\,dx \\[2mm] & = & \lim_{\beta\rightarrow\infty} \left. \frac{1}{1-s} x^{1-s} \right|_{x=1}^{x=\beta} \\[2mm] & = & \lim_{\beta\rightarrow\infty} \frac{1}{1-s} \beta^{1-s} - \frac{1}{1-s} \\[2mm] & = & \frac{1}{s-1} - \frac{1}{s-1} \lim_{\beta\rightarrow\infty} \frac{1}{\beta^{s-1}} \end{eqnarray*} Wegen $s > 1$ folgt aber $\lim_{\beta\rightarrow\infty} b^{s-1} = \infty$ und somit $\lim_{\beta\rightarrow\infty} \frac{1}{\beta^{s-1}} = 0$.
Also gilt \[ \int_1^\infty \frac{1}{x^s}\,dx = \frac{1}{s-1}, \] womit nach dem Integralkriterium die Reihe \[ \sum_{n=1}^\infty \frac{1}{n^s} \] konvergent ist.
Als nächstes betrachten wir eine Reihe, deren Summanden zwar stärker fallen als $\frac{1}{n}$ aber nicht so stark wie $\displaystyle\frac{1}{n^s}$ für $s > 1$.
Beispiel 2
Wir wollen entscheiden, ob die Reihe \[ \sum_{n=2}^\infty \frac{1}{n\log(n)} \] konvergent ist oder nicht.
Beachte, dass die Reihe erst bei Index $n=2$ beginnt. Für die Anwendung des Integralkriteriums spielt dies aber keine Rolle, denn durch Indexverschiebung können wir daraus theoretisch immer eine Reihe ab $n=1$ machen: \[ \sum_{n=2}^\infty f(n) \] konvergiert genau dann, wenn \[ \sum_{n=1}^\infty f(n+1) \] konvergiert. Ebenso konvergiert \[ \int_2^\infty f(x)\,dx \] genau dann, wenn \[ \int_1^\infty f(x+1)\,dx \] konvergiert, was sich mit der Substitutionsregel ganz einfach zeigen lässt. Wir können daher das Integralkriterium mit jedem beliebigen Startindex nutzen, nicht nur mit $n=1$.
Die Voraussetzungen für das Integralkriterium sind erfüllt: \[ f(n) = \frac{1}{n\log(n)} \] ist auf $[2,\infty)$ eine monoton fallende und nicht negative Regelfunktion.
Zur Ermittlung der Stammfunktion verwenden wir Substitution. Wir setzen \[ f(y) = \frac{1}{y} \Rightarrow F(y) = \log(y) \quad \text{sowie}\quad y=g(x)=\log(x) \Rightarrow dy=g'(x) = \frac{1}{x} \] und erhalten damit \[ \int \frac{1}{x\log(x)}\,dx = \int \frac{1}{x}\cdot\frac{1}{\log(x)}\,dx = \log(\log(x)) + c. \] Damit ergibt sich \begin{eqnarray*} \int_2^\infty \frac{1}{x\log(x)}\,dx & = & \lim_{\beta\rightarrow\infty} \int_2^\beta \frac{1}{x\log(x)}\,dx \\[2mm] & = & \lim_{\beta\rightarrow\infty} \left. \log(\log(x))\right|_{x=2}^{x=\beta} \\[2mm] & = & \lim_{\beta\rightarrow\infty} \log(\log(\beta)) - \log(\log(2)) \\[2mm] & = & \infty. \end{eqnarray*}
Die Reihe \[ \sum_{n=2}^\infty \frac{1}{n\log(n)} \] ist somit divergent.
Beweis des Integralkriteriums
Wir werden das Integralkriterium nun beweisen. Dies machen wir in zwei Schritten. Zunächst werden wir zeigen, dass die Aussage (i) des Integralkriteriums aus Aussage (ii) gefolgert werden kann. Anschließend beweisen wir dann Aussage (ii).
Lemma
Für das Integralkriterium gilt: Aussage (ii) $\Rightarrow$ Aussage (i).Beweis
Zur Erinnerung: Die beiden Aussagen lauten:
-
$\displaystyle \sum_{n=1}^\infty f(n)$ konvergiert genau dann, wenn $\displaystyle \int_1^\infty f(x)\,dx$ konvergiert.
-
Die Folge $(a_n)$ mit \[ a_n = \sum_{k=1}^n f(k) - \int_1^{n+1} f(x)\,dx \] ist konvergent.
Es gelte die Aussage (ii).
Wir definieren die Folgen $(b_n)$ und $(c_n)$ durch \begin{eqnarray*} b_n & = & \sum_{k=1}^n f(k) \\ c_n & = & \int_1^{n+1} f(x)\,dx \end{eqnarray*} Mit diesen Definitionen gilt dann \[ a_n = b_n - c_n. \]
Es sei nun $(b_n)$ konvergent. Da $(a_n)$ nach Vorausetzung konvergent ist und $c_n = b_n - a_n$ gilt, folgt mit Grenzwertregeln, dass auch $c_n$ konvergent ist.
Es sei nun $(c_n)$ konvergent. Da $(a_n)$ nach Vorausetzung konvergent ist und $b_n = a_n + c_n$ gilt, folgt mit Grenzwertregeln, dass auch $b_n$ konvergent ist.
Also ist $(b_n)$ genau dann konvergent, wenn auch $(c_n)$ konvergent ist. D. h. \[ \lim_{n\rightarrow\infty} \sum_{k=1}^n f(k) \text{ existiert } \Longleftrightarrow \lim_{n\rightarrow\infty} \int_1^{n+1} f(x)\,dx \text{ existiert,} \] woraus sich \[ \sum_{n=1}^\infty f(n) \text{ konvergiert } \Longleftrightarrow \int_1^\infty f(x)\,dx \text{ konvergiert } \] ergibt.
Damit ist das Lemma bewiesen.
Jetzt beweisen wir die Aussage (ii) des Integralkriteriums.
Beweis (Integralkriterium Aussage (ii))
Die nachfolgende Skizze ist für das Verständnis des Beweises sehr hilfreich.
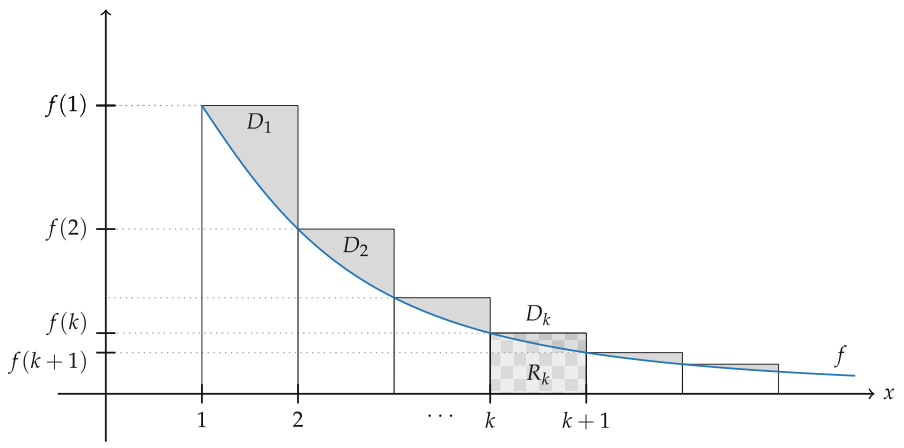
Wir definieren für den Beweis nun verschiedene Größen. Es sei:
-
$R_k := f(k)$
Dies entspricht der Fläche der $k$-ten Säule.
-
$D_k := R_k - \int_k^{k+1} f(x)\,dx = f(k) - \int_k^{k+1} f(x)\,dx$
Dies ist die Größe der dreiecksförmigen Fläche im oberen Bereich einer Säule.
Damit gilt dann \[ a_n = \sum_{k=1}^n f(k) - \int_1^{n+1} f(x)\,dx = \sum_{k=1}^n \left( f(k) - \int_k^{k+1} f(x)\,dx\right) = \sum_{k=1}^n D_k. \] Das Folgenglied $a_n$, das ja die Differenz zwischen Partialsumme und Integral bis zur Stelle $n+1$ darstellt, ist demnach die Summe der ersten $n$ Dreiecksflächen.
Um zu zeigen, dass $(a_n)$ eine konvergente Folge ist, nutzen wir den Satz der monotonen Konvergenz. Wir müssen also zeigen, dass die Folgenglieder $a_n$ monoton und beschränkt sind.
Monotonie: Nach Voraussetzung ist die Funktion $f$ monoton fallend. Daher gilt $f(x) \leq f(k)$ für $x \in [k,k+1]$. Mit der Monotonie des Integrals folgt \[ \int_k^{k+1} f(x)\,dx \leq ((k+1) - k) \cdot f(k) = f(k). \] Daraus ergibt sich $D_k \geq 0$, womit \[ a_n = \sum_{k=1}^n D_k \] monoton wachsend ist.
Beschränktheit: Man kann anschaulich sehr schön begründen, dass die Gesamtfläche der $D_k$ beschränkt ist. Schaue Dir dazu die obige Skizze an. Wenn Du jetzt alle $D_k$-Flächen horizontal in die erste Säule (ganz links) verschiebst, liegen sie dort alle disjunkt zueinander. Das heißt, das die Gesamtfläche der $D_k$ nicht größer als die Fläche der ersten Säule ist. Somit ist $f(1)$ immer eine obere Schranke für $\sum_{k=1}^n D_k$ und somit für $a_n$.
Wir können diese Schranke aber auch leicht formal herleiten. Zunächst gilt \[ 0 \leq D_k = f(k) - \int_k^{k+1} f(x)\,dx \leq f(k) - f(k+1). \] Für die Abschätzung haben wir $\int_k^{k+1} f(x)\,dx$ durch die Fläche der nächsten Säule ersetzt, die auf jeden Fall kleiner ist. Damit folgt dann \[ 0 \leq a_n = \sum_{k=1}^n D_k \leq \sum_{k=1}^n (f(k) - f(k+1)) \stackrel{\text{Teleskopsumme}}{=} f(1) - f(n+1) \leq f(1). \]
Also sind die $a_n$ monoton und beschränkt und somit ist $(a_n)$ eine konvergente Folge.
Damit ist Aussage (ii) bewiesen. Mit dem vorangegengenen Lemma folgt, dass somit auch Aussage (i) gilt.
Teilen und Drucken