In der vorigen Blog-Folge hast Du gelernt, dass eine stetige, streng monotone Funktion eine Umkehrfunktion besitzt und diese dann wieder stetig und streng monoton ist. In dieser Blog-Folge betrachten wir dies am Beispiel der Exponentialfunktion.
Existenz der Umkehrfunktion
Die Exponentialfunktion ist stetig und streng monoton wachsend. Beides haben wir bereits gezeigt. Dabei haben wir die Stetigkeit der Exponentialfunktion gleich in der ersten Blog-Folge des Kapitels bewiesen, deren strenge Monotonie in der vorangegangenen Blog-Folge. Die Exponentialfunktion ist streng monoton wachsend.
Mit dem zentralen Satz der vorangegangenen Blog-Folge folgt, dass die Exponentialfunktion auf jedem abgeschlossenem Intervall der reellen Zahlen eine Umkehrfunktion besitzt. Wir wollen diese Aussage nun noch ein wenig verallgemeinern und den zugehörigen Bildbereich genau charakterisieren.
Auch wenn jedes abgeschlossenem Intervall eine echte Teilmenge der reellen Zahlen bildet, so können wir trotzdem davon ausgehen, dass auf ganz $\R$ eine Umkehrfunktion existiert. Die strenge Monotonie garantierte uns die Injektivität. Da die Exponentialfunktion auf ganz $\R$ streng monoton ist, ist sie dort auch injektiv. Stetig ist sie ebenfalls auf ganz $\R$. Bleibt noch, den Bildbereich so weit einzuschränken, dass wir Surjektivität garantieren können.
Für $x > 0$ gilt \[ \exp(x) = \sum_{n=0}^\infty \frac{x^n}{n!} = 1 + x + \sum_{n=2}^\infty \frac{x^n}{n!} \geq 1 + x \] und \[ \lim_{x\rightarrow\infty} 1 + x = \infty. \] Damit folgt auch \[ \lim_{x\rightarrow\infty} \exp(x) = \infty. \] Weiterhin gilt damit \[ 0 < \exp(-x) = \frac{1}{\exp(x)} \leq \frac{1}{1+x}. \] Wegen $\lim_{x\rightarrow\infty} \frac{1}{1+x} = 0$ folgt damit \[ \lim_{x\rightarrow -\infty} \exp(x) = 0. \] Die Stetigkeit garantiert uns, dass es keine Lücken gibt (Zwischenwertsatz). Weiterhin wissen wir, dass auch $\exp(x) > 0$ für alle $x\in\R$ gilt, womit \[ \exp(\R) = \R_+ \] folgt. Das Bild der Exponentialfunktion besteht also aus den positiven reellen Zahlen.
Logarithmusfunktion
Im letzten Abschnitt haben wir gesehen, dass die Expoentialfunktion $\R$ bijektiv auf $\R_+$ abbildet. Die zugehörige Umkehrfunktion nennen wir Logarithmus.
Definition
Die Funktion \[ \log: \R_+ \rightarrow \R \] sei die Umkehrfunktion der Exponentialfunktion. Die Funktion heißt der (natürliche) Logarithmus.Wir werden den Logarithmus unter anderem dazu nutzen, Potenzen $a^x$ für $x\in\R$ zu definieren. Die Exponentialfunktion entspricht dann der Funktion $\e^x$. Potenzfunktionen wie $f(x) = a^x$ für $a > 0$ haben auch eine Umkehrfunktion, die wir auch Logarithmus nennen und die wir später noch genau definieren. Wenn wir deutlich machen möchten, dass wir speziell die Umkehrfunktion der Exponentialfunktion meinen, sprechen wir auch vom natürlichen Logarithmus.
Aus dem zentralen Satz der letzten Blog-Folge ergeben sich zwei wesentliche Eigenschaften des Logarithmus.
Korollar
Die Funktion \[ \log: \R_+ \rightarrow \R \] ist stetig und streng monoton wachsend.Hier ein Funktionsgraph der Logarithmusfunktion:
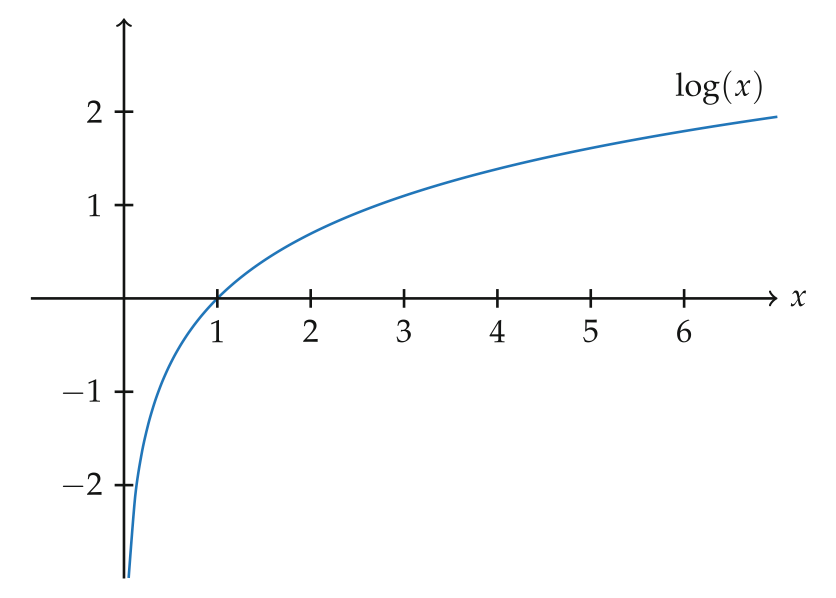
Wir sehen, dass $\log(1) = 0$ gilt, wegen $\exp(0) = 1$. Weiterhin gilt \[ \lim_{x\rightarrow 0} = -\infty \] und \[ \lim_{x\rightarrow \infty} = \infty, \] was wir später noch genau beweisen werden.
Additionstheorem
Eine bedeutende Eigenschaft der Exponentialfunktion ist das Additionstheorem \[ \exp(x+y) = \exp(x) \cdot \exp(y). \] Für den Logarithmus gilt ein ähnliches Additionstheorem.
Satz
Für alle $x,y \in\R_+$ gilt \[ \log(xy) = \log(x) + \log(y). \]Während bei der Exponentialfunktion der Funktionswert der Summe der Argumente mit dem Produkt der einzelnen Funktionswerte identisch ist, sind demgegenüber beim Logarithmus Summenbildung und Produkt vertauscht. Hier ist jetzt der Funktionswert des Produktes $xy$ mit der Summe der einzelnen Funktionswerte identisch.
Beweis
Es seien $x,y\in\R_+$ beliebig.
Dann existieren eindeutig bestimmte Zahlen $\alpha,\beta\in\R$ mit \[ x = \exp(\alpha) \quad\text{und}\quad y = \exp(\beta) \] und somit \[ \log(x) = \alpha \quad\text{und}\quad \log(y) = \beta. \] Es folgt \begin{eqnarray*} \log(xy) & = & \log(\exp(\alpha)\exp(\beta)) \\ & = & \log(\exp(\alpha + \beta)) \\ & = & \alpha + \beta \\ & = & \log(x) + \log(y). \end{eqnarray*}
In der nächsten Blog-Folge werden wir den Logarithmus nutzen, um zu definieren, was wir unter $a^x$ für $x\in\R$ verstehen. Damit werden wir dann auch die bekannten Potenzgesetze beweisen.
Teilen und Drucken