Bestimmte Integrale entsprechen dem Inhalt von beschränkten Flächen. Die Integralrechnung erlaubt es uns aber auch, den Flächeninhalt von unbeschränkten Flächen zu ermiteln. Dies geschieht mit sogenannten uneigentlichen Integralen. In dieser Blog-Folge zeige ich Dir, was uneigentliche Integrale sind und wie man sie berechnet.
Motivation
Bisher haben wir stets Integrale auf einem abgeschlossenen Intervall $[a,b]$ betrachtet. Wenn die Funktion $f(x)$, über die das Integral gebildet wird, auf dem Intervall $[a,b]$ nicht negativ ist, dann stimmt der Wert des bestimmten Integrals \[ \int_a^b f(x)\,dx \] mit dem Flächeninhalt der Fläche überein, die nach links durch $a$, nach rechts durch $b$, nach oben durch den Funktionsgraphen und nach unten durch die $x$-Achse beschränkt ist. Damit ist die Fläche, die dem Wert des Integrals entspricht, insbesondere eine beschränkte Fläche, d. h. wir können die Fläche mit einem Kreis, der einen endlichen Radius hat, umschließen.
Demgegenüber entsprechen uneigentliche Integrale Flächen, die nicht beschränkt sind. Zum Beispiel:
Wie groß ist der Flächeninhalt der Fläche, die durch die $y$-Achse nach links, die $x$-Achse nach unten und den Graph der Funktion $f(x) = \e^{-\frac{1}{2}x}$ nach oben begrenzt wird?
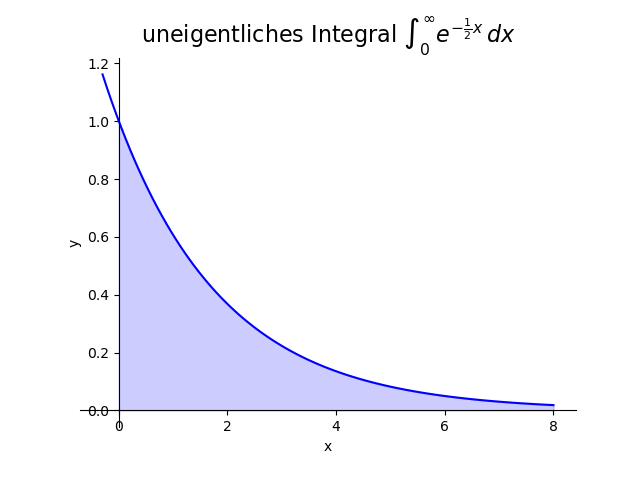
Bei dieser Fläche haben wir keine Begrenzung nach rechts, weshalb die Fläche nicht beschränkt ist. Insbesondere ist es nicht möglich, sie in einen Kreis mit endlichem Radius einzuschließen.
Du könntest auf die Idee kommen, dass solch eine nicht beschränkte Fläche einen Flächeninhalt haben muss, der unendlich groß ist. Dies kann, muss aber nicht der Fall sein. Wir kennen dies schon von Reihen, die ja unendlich viele Summanden haben. Obwohl wir unendlich viele Summanden haben, muss die Gesamtsumme all dieser Summanden nicht unendlich groß werden. Stattdessen berechnen wir die aus unendlichen vielen Summanden bestehende Gesamtsumme mit einem Grenzwert.
Für die Berechnung des Flächeninhalts von unbeschränkten Flächen werden wir ebenfalls Grenzwerte nutzen. Wie bei der Berechnung von Grenzwerten üblich, können diese Grenzwerte existieren oder aber auch nicht. Ich demonstriere dies am Beispiel der obigen Frage.
Beispiel 1
Für jede feste rechte Grenze $\beta$ können wir das bestimmte Integral von $0$ bis $\beta$ über die Funktion $f(x) = \e^{-\frac{1}{2}x}$ berechnen: \begin{eqnarray*} \int_0^\beta \e^{-\frac{1}{2}x}\,dx & = & \left.-2\e^{-\frac{1}{2}x} \right|_{x=0}^{x=\beta} \\[3mm] & = & -2\e^{-\frac{1}{2}\beta} + 2\e^0 \\[3mm] & = & 2\left(1-\e^{-\frac{1}{2}\beta}\right). \end{eqnarray*} Jetzt lassen wir die rechte Grenze $\beta$ gegen $\infty$ laufen. Dann ergibt sich \begin{eqnarray*} \lim_{\beta\rightarrow\infty} \int_0^\beta \e^{-\frac{1}{2}x}\,dx & = & \lim_{\beta\rightarrow\infty} 2\left(1-\underbrace{\e^{-\frac{1}{2}\beta}}_{\rightarrow 0}\right) \\[3mm] & = & 2. \end{eqnarray*} Also beträgt der Gesamtflächeninhalt der unbeschränkten Fläche $2$.Definition
Beispiel 1 hat gezeigt, wie wir den Flächeninhalt einer unbeschränkten Flächen berechnen können. Dabei war dort die Unbeschränktheit durch die fehlende rechte Grenze gegeben. Neben einer fehlenden rechten Grenze kann aber auch eine fehlende linke Grenze oder eine Polstelle zu einer unbeschränkten Fläche führen. Die nachfolgende Definition für uneigentliche Integrale berücksichtigt all diese Fälle.
Definition
Seien $-\infty\leq a < b\leq\infty$ und sei $f:(a,b)\rightarrow\R$ eine Regelfunktion.
Wir nennen $\int_a^b f(x)\,dx$ ein uneigentliches Integral und definieren:
- Falls $f$ bei $a$ definiert und auf $[a,b)$ Regelfunktion ist, sei \[ \int_a^b f(x)\,dx := \lim_{\beta\nearrow b} \int_a^\beta f(x)\,dx. \]
- Falls $f$ bei $b$ definiert und auf $(a,b]$ Regelfunktion ist, sei \[ \int_a^b f(x)\,dx := \lim_{\alpha\searrow a} \int_\alpha^b f(x)\,dx. \]
- Im Allgemeinen: Wähle $c\in(a,b)$ und definiere: \[ \int_a^b f(x)\,dx := \int_a^c f(x)\,dx + \int_c^b f(x)\,dx. \]
Falls der Grenzwert jeweils existiert und endlich ist, sagen wir, dass das uneigentliche Integral konvergiert.
Die drei Fälle der Definition behandeln die drei Situationen, die bei uneigentlichen Integralen auftreten können. In Fall (i) ist die Funktion $f(x)$ an der linken Integrationsgrenze $a$ definiert, aber nicht an der rechten Grenze $b$. Das heißt, die rechte Grenze $b$ ist eine Polstelle oder, so wie in Beispiel 1, gleich $\infty$.
Wenn die rechte Integrationsgrenze gleich $\infty$ ist, dann dürfen wir statt des linksseitigen Grenzwertes \[ \lim_{\beta \nearrow \infty} \int_a^\beta f(x)\,dx \] für $\beta$ auch \[ \lim_{\beta \rightarrow \infty} \int_a^\beta f(x)\,dx \] schreiben.
In Fall (ii) ist die Funktion $f(x)$ an der rechten Integrationsgrenze $b$ definiert aber nicht an der linken Integrationsgrenze $a$. Hier ist also die linke Integrationsgrenze $a$ eine Polstelle oder gleich $-\infty$.
Ist die Funktion $f(x)$ weder an der rechten noch an der linken Integrationsgrenze definiert, weil es sich um Polstellen oder $\pm \infty$ handelt, dann wählt man einen beliebigen Zwischenpunkt $c$ und teilt das uneigentliche Integral in zwei uneigentliche Integrale auf. Für das erste uneigentliche Integral liegt dann Fall (ii) und für das zweite uneigentliche Integral Fall (i) vor. Dabei ist der Wert der Summe immer unabhängig von der Wahl des Zwischenpunkts $c$.
Ich demonstriere die Definition des uneigentlichen Integrals an einer Reihe von Beispielen.
Beispiel 2
Wir wollen \[ \int_1^\infty \frac{1}{x^2}\,dx \] berechnen. Es liegt Fall (i) aus der Definition vor, denn die Funktion $f(x) = \frac{1}{x^2}$ ist an der linken Integrationsgrenze $1$ definiert, während die rechte Grenze gleich $\infty$ ist.
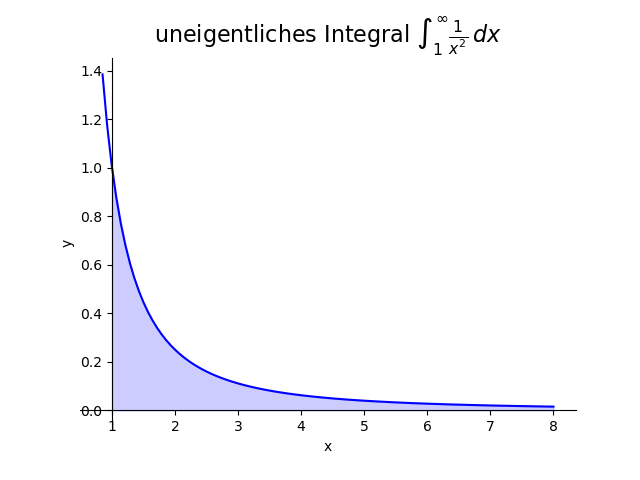
Somit ergibt sich \begin{eqnarray*} \int_1^\infty \frac{1}{x^2}\,dx & = & \lim_{\beta\rightarrow\infty} \int_1^\beta \frac{1}{x^2}\,dx \\[3mm] & = & \lim_{\beta\rightarrow\infty} \left. -\frac{1}{x}\right|_{x=1}^{x=\beta} \\[3mm] & = & \lim_{\beta\rightarrow\infty} -\frac{1}{\beta} + 1 \\[3mm] & = & 1. \end{eqnarray*}
Beispiel 3
Wir wollen \[ \int_1^\infty \frac{1}{x}\,dx \] berechnen. Es liegt wieder Fall (i) vor und es gilt \begin{eqnarray*} \int_1^\infty \frac{1}{x}\,dx & = & \lim_{\beta\rightarrow\infty} \int_1^\beta \frac{1}{x}\,dx \\[3mm] & = & \lim_{\beta\rightarrow\infty} \log(x)|_{x=1}^{x=\beta} \\[3mm] & = & \lim_{\beta\rightarrow\infty} \log(\beta) \\[3mm] & = & \infty. \end{eqnarray*} Dieses uneigentliche Integral konvergiert also nicht.
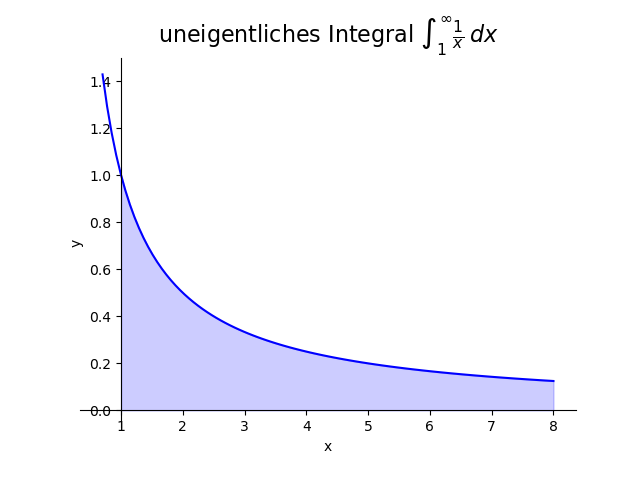
Beispiel 4
Wir wollen \[ \int_0^1 \frac{1}{\sqrt{x}}\,dx \] bestimmen. Diesmal liegt Fall (ii) vor, denn $f(x) = \frac{1}{\sqrt{x}}$ hat an der linken Integrationsgrenze $0$ eine Polstelle und ist an der rechten Grenze $1$ definiert.
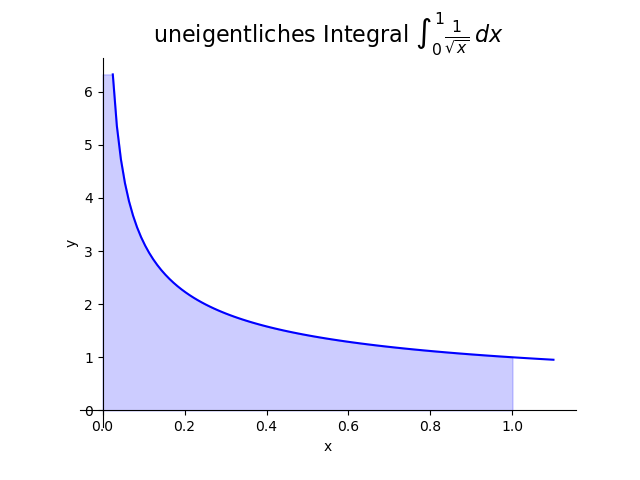
Es gilt \begin{eqnarray*} \int_0^1 \frac{1}{\sqrt{x}}\,dx & = & \lim_{\alpha\searrow 0} \int_\alpha^1 \frac{1}{\sqrt{x}}\,dx \\[3mm] & = & \lim_{\alpha\searrow 0} \left. 2\sqrt{x}\right|_{x=\alpha}^{x=1} \\[3mm] & = & \lim_{\alpha\searrow 0} 2-2\sqrt{\alpha} \\[3mm] & = & 2. \end{eqnarray*}
Beispiel 5
Wir wollen \[ \int_{-\infty}^\infty |x| \e^{-\frac{1}{2}x^2}\,dx \] bestimmen. Hier liegt Fall (iii) vor.
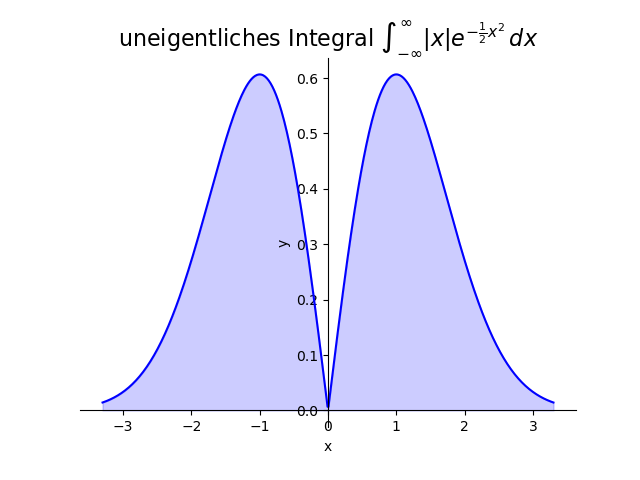
Wir wählen $c=0$ und erhalten damit: \begin{eqnarray*} \int_{-\infty}^\infty |x| \e^{-\frac{1}{2}x^2}\,dx & = & \int_{-\infty}^0 |x| \e^{-\frac{1}{2}x^2}\,dx + \int_0^\infty |x| \e^{-\frac{1}{2}x^2}\,dx \\[3mm] & = & \int_{-\infty}^0 (-x) \e^{-\frac{1}{2}x^2}\,dx + \int_0^\infty x \e^{-\frac{1}{2}x^2}\,dx \\[3mm] & = & \lim_{\alpha\rightarrow -\infty} \int_\alpha^0 (-x) \e^{-\frac{1}{2}x^2}\,dx + \lim_{\beta\rightarrow\infty} \int_0^\beta x \e^{-\frac{1}{2}x^2}\,dx \\[3mm] & = & \lim_{\alpha\rightarrow -\infty} \left. \e^{-\frac{1}{2}x^2} \right|_{x=\alpha}^{x=0} + \lim_{\beta\rightarrow\infty} \left. -\e^{-\frac{1}{2}x^2} \right|_{x=0}^{x=\beta} \\[3mm] & = & \lim_{\alpha\rightarrow -\infty} \left( 1-\e^{-\frac{1}{2}\alpha^2} \right) + \lim_{\beta\rightarrow\infty} \left( -\e^{-\frac{1}{2}\beta^2} + 1 \right) \\[3mm] & = & 2. \end{eqnarray*}
Beispiel 6
Wir wollen \[ \int_0^1 \frac{1}{\sqrt{x}} + \frac{1}{\sqrt{1-x}}\,dx \] berechnen. Es liegt zwar wieder Fall (iii) vor, aber im Gegensatz zu Beispiel 5 haben wir hier zwei Polstellen an den Integrationsgrenzen.
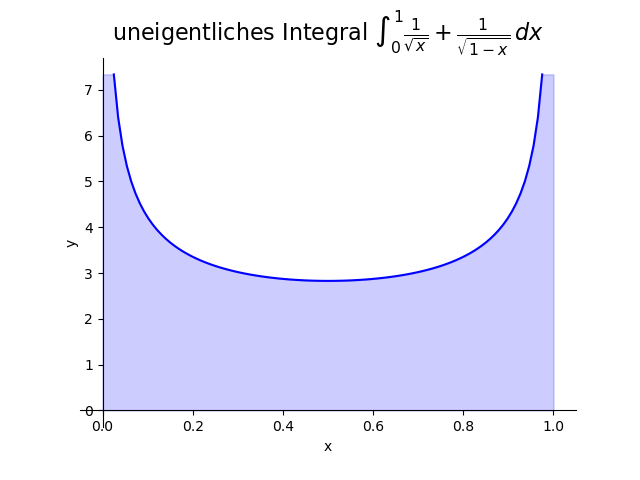
Wir wählen $c = \frac{1}{2}$ und erhalten: \begin{eqnarray*} \int_0^1 \frac{1}{\sqrt{x}} + \frac{1}{\sqrt{1-x}}\,dx & = & \int_0^\frac{1}{2} \frac{1}{\sqrt{x}} + \frac{1}{\sqrt{1-x}}\,dx + \int_\frac{1}{2}^1 \frac{1}{\sqrt{x}} + \frac{1}{\sqrt{1-x}}\,dx \\[3mm] & = & \lim_{\alpha\searrow 0} \int_\alpha^\frac{1}{2} \frac{1}{\sqrt{x}} + \frac{1}{\sqrt{1-x}}\,dx + \lim_{\beta\nearrow 1} \int_\frac{1}{2}^\beta \frac{1}{\sqrt{x}} + \frac{1}{\sqrt{1-x}}\,dx \\[3mm] & = & \lim_{\alpha\searrow 0} \left[2\sqrt{x} - 2\sqrt{1-x}\right]_{x=\alpha}^{x=\frac{1}{2}} + \lim_{\beta\nearrow 1} \left[2\sqrt{x} - 2\sqrt{1-x}\right]_{x=\frac{1}{2}}^{x=\beta} \\[3mm] & = & \lim_{\alpha\searrow 0} \left( 2\sqrt{\frac{1}{2}} - 2\sqrt{\frac{1}{2}} - 2\sqrt{\alpha} + 2\sqrt{1-\alpha} \right) + \lim_{\beta\nearrow 1} \left( 2\sqrt{\beta} - 2\sqrt{1-\beta} - 2\sqrt{\frac{1}{2}} + 2\sqrt{\frac{1}{2}} \right) \\[3mm] & = & 2 + 2 \\[3mm] & = & 4. \end{eqnarray*}
Majorantenkriterium für uneigentliche Integrale
Von Reihen kennen wir den Begriff der absoluten Konvergenz sowie Konvergenzkriterien für die absolute Konvergenz, z. B. das Majorantenkriterium. Diese Konzepte lassen sich auf uneigentliche Integrale übertragen.
Definition
Seien $-\infty \leq a < b \leq \infty$ und $f:(a,b) \rightarrow\R$ eine Regelfunktion.
Wenn das uneigentliche Integral \[ \int_a^b |f(x)|\,dx \] konvergiert, dann heißt das uneigentliche Integral $\int_a^b f(x)\,dx$ absolut konvergent.
Wie bei Reihen folgt auch bei uneigentlichen Integralen aus der absoluten Konvergenz die Konvergenz.
Proposition
Wenn ein uneigentliches Integral \[ \int_a^b f(x)\,dx \] absolut konvergent ist, dann ist es auch konvergent.Der folgende Satz beschreibt das Majorantenkriterium für uneigentliche Integrale.
Satz
Seien $-\infty \leq a < b \leq \infty$ und $f,g:(a,b)\rightarrow\R$ Regelfunktionen.
Gilt
- $|f(x)|\leq g(x)$ für alle $x\in(a,b)$ und
- $\int_a^b g(x)\,dx$ konvergiert,
Das folgende Beispiel zeigt eine einfache Anwendung des Majorantenkriteriums.
Beispiel 7
Konvergiert \[ \int_0^\infty \frac{1}{x^2 + 3x + 5}\,dx\,? \]
Zunächst gilt \[ \int_0^\infty \frac{1}{x^2 + 3x + 5}\,dx = \int_0^1 \frac{1}{x^2 + 3x + 5}\,dx + \int_1^\infty \frac{1}{x^2 + 3x + 5}\,dx. \] Das linke Integral der Summe auf der rechten Seite ist ein bestimmtes Integral. Dementsprechend konvergiert das Ausgangsintegral genau dann, wenn das rechte uneigentliche Integral der Summe konvergiert.
Für dieses Integral wenden wir das Majorantenkriterium an. Es gilt \[ 0 < \frac{1}{x^2 + 3x + 5} \leq \frac{1}{x^2} \] für alle $x\in[1,\infty)$. Außerdem hatten wir in Beispiel 2 gezeigt, dass \[ \int_1^\infty \frac{1}{x^2}\,dx \] konvergiert. Also folgt mit dem Majorantenkriterium, dass auch \[ \int_1^\infty \frac{1}{x^2 + 3x + 5}\,dx \] und somit auch \[ \int_0^\infty \frac{1}{x^2 + 3x + 5}\,dx \] konvergiert.
Im nächsten Beispiel untersuchen wir ein uneigentliches Integral, das zwar konvergent aber nicht absolut konvergent ist.
Beispiel 8
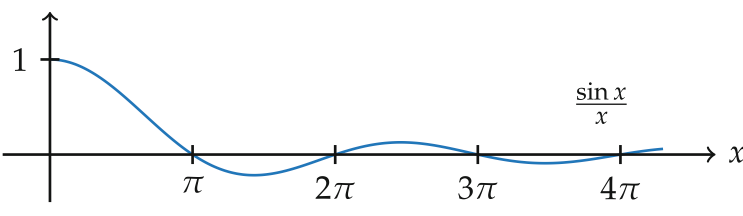
Konvergiert \[ \int_0^\infty \frac{\sin(x)}{x}\,dx\,? \]
Beachte, dass bei $x=0$ keine Polstelle vorliegt sondern die Funktion $f(x) = \frac{\sin(x)}{x}$ stetig fortsetzbar ist. Hier ein Bild des Funktionsgraphen:
1. Versuch
Wegen $-1 \leq \sin(x) \leq 1$ gilt \[ \left| \frac{\sin(x)}{x} \right| \leq \frac{1}{x}. \] Die Funktion $g(x) = \frac{1}{x}$ ist also eine Majorante für $f(x) = \frac{\sin(x)}{x}$.
Leider konvergiert aber schon das Integral \[ \int_1^\infty \frac{1}{x}\,dx \] nicht, wie wir schon in Beispiel 3 gezeigt haben. Dieser Ansatz ist also nicht zielführend. Er ist zu einfach.
2. Versuch
Wir teilen das Integral zuerst in einen bestimmten und einen uneigentlichen Teil auf. \[ \int_0^\infty \frac{\sin(x)}{x}\,dx = \int_0^1 \frac{\sin(x)}{x}\,dx + \int_1^\infty \frac{\sin(x)}{x}\,dx. \] Damit konvergiert das ursprüngliche uneigentliche Integral genau dann, wenn das uneigentliche Integral \[ \int_1^\infty \frac{\sin(x)}{x}\,dx \] konvergiert.
Jetzt wenden wir einmal partielle Integration an: \begin{eqnarray*} & & \lim_{\beta\rightarrow\infty} \int_1^\beta \frac{\sin(x)}{x}\,dx = \lim_{\beta\rightarrow\infty} \int_1^\beta \frac{1}{x} \sin(x)\,dx \\ & = & \lim_{\beta\rightarrow\infty}\left(\left.\frac{1}{x}\cdot(-\cos(x))\right|_{x=1}^{x=\beta} - \int_1^\beta \left(-\frac{1}{x^2}\right) (-\cos(x))\,dx\right) \\ & = & \lim_{\beta\rightarrow\infty} \frac{1}{\beta}(-\cos(\beta))+\cos(1) - \int_1^\infty \frac{1}{x^2}\cos(x)\,dx \\ & = & \cos(1) - \int_1^\infty \frac{1}{x^2}\cos(x)\,dx \end{eqnarray*} Damit bleibt nur noch die Frage, ob \[ \int_1^\infty \frac{1}{x^2}\cos(x)\,dx \] konvergiert. Dies ist aber der Fall, denn es gilt \[ \left| \frac{\cos(x)}{x^2} \right| \leq \frac{1}{x^2}, \] und wir hatten in Beispiel 2 gezeigt, dass \[ \int_1^\infty \frac{1}{x^2}\,dx \] konvergent ist. Also konvergiert das uneigentliche Integral $\int_1^\infty \frac{1}{x^2}\cos(x)\,dx$ nach dem Majorantenkriterium und somit auch \[ \int_0^\infty \frac{\sin(x)}{x}\,dx. \]
Tatsächlich ist das Integral zwar konvergent, aber nicht absolut konvergent. Durch die Anwendung der partiellen Integration konnten wir die Frage der Konvergenz aber trotzdem mit dem Majorantenkriterium beantworten.
Bei der Betrachtung der verschiedenen Beispiele konnten wir schon einige Analogien zwischen Reihen und uneigentlichen Integralen feststellen. So ist beispielsweise sowohl die Reihe \[ \sum_{n=1}^\infty \frac{1}{n^2} \quad \text{als auch das uneigentliche Integral} \quad \int_1^\infty \frac{1}{x^2}\,dx \] konvergent. Ebenso ist sowohl die Reihe \[ \sum_{n=1}^\infty \frac{1}{n} \quad \text{als auch das Integral} \quad \int_1^\infty \frac{1}{x}\,dx \] divergent. Weiterhin haben wir das Majorantenkriterium für uneigentliche Integrale kennengelernt, das analog zum Majorantenkriterium für Reihen formuliert ist und die absolute Konvergenz garantiert.
In der nächsten Blog-Folge nutzen wir diese Analogien aus, um ein weiteres Kriterium für die Konvergenz von Reihen zu formulieren und zu beweisen, das auf uneigentlichen Integralen basiert.
Teilen und Drucken