Leider ist es uns nicht immer möglich, zu einer Funktion eine Stammfunktion in elementarer Form zu konstruieren. Hier können uns Potenzreihen weiterhelfen.
Motivation
Leider ist es uns nicht immer möglich, zu einer Funktion deren Stammfunktion zu bestimmen. Nicht nur, weil wir vielleicht nicht den richtigen Weg finden, um eine Stammfunktion zu konstruieren, sondern auch, weil es für eine Reihe von Funktionen keine Stammfunktion in elementarer Form gibt. Dies lässt sich tatsächlich mathematisch beweisen. Dabei bedeutet "in elementarer Form" als arithmetische Kombination oder Verkettung von elementaren Funktionen, wie Polynomen, Exponentialfunktion, Sinus, Cosinus, etc. oder deren Umkehrfunktionen.
Nun betrifft dies nicht nur exotische Funktionen, sondern auch einige in der Mathematik äußerst wichtige Funktionen besitzen keine Stammfunktion in elementarer Form. Ein bekanntes Beispiel hierfür ist die vielleicht wichtigste Funktion der Statistik, die Dichtefunktion der Standardnormalverteilung. Sie lautet \[ f(x) = \frac{1}{\sqrt{2\pi}} \e^{-\frac{1}{2}x^2}. \]
Gerade in der Wahrscheinlichkeitstheorie und Statistik ist die Integralrechnung aber von fundamentaler Bedeutung. So ist beispielsweise die Wahrscheinlichkeit $P(a \leq X \leq b)$, dass eine standardnormalverteile Zufallsvariable $X$ einen Wert zwischen $a$ und $b$ annimmt, gleich \[ \int_a^b \frac{1}{\sqrt{2\pi}} \e^{-\frac{1}{2}x^2}\,dx, \] also gleich dem Integral von $a$ bis $b$ über die Dichtefunktion der Standardnormalverteilung.
Aber wie können wir nun solch ein Integral berechnen, wenn wir keine Stammfunktion haben? Eine Möglichkeit besteht darin, Potenzreihen zu nutzen und zumindest eine Stammfunktion in Form einer Potenzreihe zu konstruieren.
Stammfunktionen für Potenzreihen
Zu einer Potenzreihe mit einem Konvergenzradius $R > 0$ können wir leicht eine Stammfunktion angeben.
Satz 1
Wenn die Potenzreihe \[ f(x) = \sum_{n=0}^\infty a_n (x-x_0)^n \] den Konvergenzradius $R > 0$ hat, dann hat die Potenzreihe \[ F(x) = \left(\sum_{n=0}^\infty \frac{a_n}{n+1} (x-x_0)^{n+1}\right) +c \] ebenfalls den Konvergenzradius $R$ und ist eine Stammfunktion für $f$.Beweis
Der Satz folgt unmitelbar aus den Regeln zur Ableitung von Potenzreihen, siehe hier.Gemäß Satz 1 werden Potenzreihen summandenweise integriert. Damit können wir zu Funktionen, für die wir eine Potenzreihendarstellung kennen, immer eine Stammfunktion in Potenzreihendarstellung angeben.
Durch eine geschickte Wahl von $c$ ist es darüberhinaus möglich, die Stammfunktion wieder als Potenzreihe über $(x-x_0)^n$ statt $(x-x_0)^{n+1}$ und ab $n=0$ zu schreiben. Ich verdeutliche dies an einem einfachen Beispiel.
Beispiel 1
Sei \[ f(x) = \sum_{n=0}^\infty (n^2 + 3n + 2) x^n. \] Diese Potenzreihe hat den Konvergenzradius $R=1$, was Du mit dem Quotientenkriterium leicht prüfen kannst.
Nach Satz 1 gilt \[ \int \sum_{n=0}^\infty (n^2 + 3n + 2) x^n\,dx = \sum_{n=0}^\infty \int (n^2+3n+2)x^n\,dx = \sum_{n=0}^\infty (n+2) x^{n+1} + c, \] denn $(n+2)(n+1) = n^2 +3n + 2$. Mit Indexverschiebung und $c=1$ erhalten wir \[ = \sum_{n=1}^\infty (n+1) x^n + 1 = \sum_{n=0}^\infty (n+1) x^n. \]
Zur Bestätigung machen wir die Probe: \begin{eqnarray*} \left( \sum_{n=0}^\infty (n+1) x^n \right)' & = & \sum_{n=0}^\infty \left( (n+1) x^n \right)' \\[3mm] & = & \sum_{n=1}^\infty n(n+1)x^{n-1} \\[3mm] & = & \sum_{n=0}^\infty (n+1)(n+2) x^n \\[3mm] & = & \sum_{n=0}^\infty (n^2 + 3n + 2) x^n. \end{eqnarray*}
Um zu einer gegebenen Funktion $f(x)$ eine Stammfunktion in Form einer Potenzreihe anzugeben, müssen wir voher $f(x)$ als Potenzreihe darstellen. Ich zeige Dir an zwei Beispielen, wie das geht.
Beispiel 2
Wir leiten für die Dichtefunktion \[ f(x) = \frac{1}{\sqrt{2\pi}} \e^{-\frac{1}{2}x^2} \] der Standardnormalverteilung eine Stammfunktion in Potenzreihenform her. Dazu stellen wir in einem ersten Schritt die Funktion $f(x)$ als Potenzreihe dar.
Wir kennen die Potenzreihendarstellung der Exponentialfunktion: \[ \e^y = \sum_{n=0}^\infty \frac{y^n}{n!}. \] Damit ergibt sich für $y = -\frac{1}{2}x^2$: \begin{eqnarray*} \e^{-\frac{1}{2}x^2} & = & \sum_{n=0}^\infty \frac{\left( -\frac{1}{2}x^2 \right)^n}{n!} \\[3mm] & = & \sum_{n=0}^\infty \frac{(-1)^n \left(\frac{1}{2}\right)^n x^{2n}}{n!} \\[3mm] & = & \sum_{n=0}^\infty \frac{(-1)^n x^{2n}}{2^n n!}. \end{eqnarray*} Somit gilt \[ f(x) = \frac{1}{\sqrt{2\pi}} \e^{-\frac{1}{2}x^2} = \frac{1}{\sqrt{2\pi}} \sum_{n=0}^\infty \frac{(-1)^n x^{2n}}{2^n\,n!}, \] womit wir eine Potenzreihendarstellung für $f(x)$ haben.
Nun gilt \[ \int \frac{(-1)^n x^{2n}}{2^n\,n!}\,dx = \frac{(-1)^n x^{2n+1}}{(2n+1)2^n\,n!}. \] Mit Satz 1 folgt dann, dass \[ F(x) = \frac{1}{\sqrt{2\pi}} \sum_{n=0}^\infty \frac{(-1)^n x^{2n+1}}{(2n+1)2^n\,n!} \] eine Stammfunktion von $f(x)$ in Potenzreihenform ist.
Beispiel 3
Zur Bestimmung von \[ \int \sin(x^2)\,dx \] verwenden wir die Potenzreihendarstellung von \[ \sin(y) = y-\frac{y^3}{3!} + \frac{y^5}{5!} - \cdots = \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!}y^{2n+1}. \] Für $y=x^2$ ergibt dies \[ \sin(x^2) = x^2 -\frac{x^6}{3!} + \frac{x^{10}}{5!} - \cdots = \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!}x^{4n+2}. \] Also folgt mit Satz 1: \begin{eqnarray*} \int \sin(x^2)\,dx & = & \frac{x^3}{3} - \frac{x^7}{7\cdot 3!} + \frac{x^{11}}{11\cdot 5!} - \cdots \\[3mm] & = & \sum_{n=0}^\infty \frac{(-1)^n}{(4n+3)(2n+1)!} x^{4n+3}. \end{eqnarray*}Bestimmte Integrale mit Potenzreihen approximativ berechnen
Da wir nun in der Lage sind, Stammfunktionen in Potenzreihenform anzugeben, können wir dies nutzen, um Integrale zumindest approximativ zu berechnen. Ich verdeutliche dies am Beispiel des bestimmten Integrals \[ \int_{-1}^1 \frac{1}{\sqrt{2\pi}} \e^{-\frac{1}{2}x^2}, \] also einem bestimmten Integral für die Dichtefunktion der Standardnormalverteilung. Der Wert dieses Integrals ist gleich der Wahrscheinlichkeit, dass eine standardnormalverteilte Zufallsvariable einen Wert zwischen $-1$ und $1$ annimmt und entspricht dem Flächeninhalt der hellblauen Fläche.
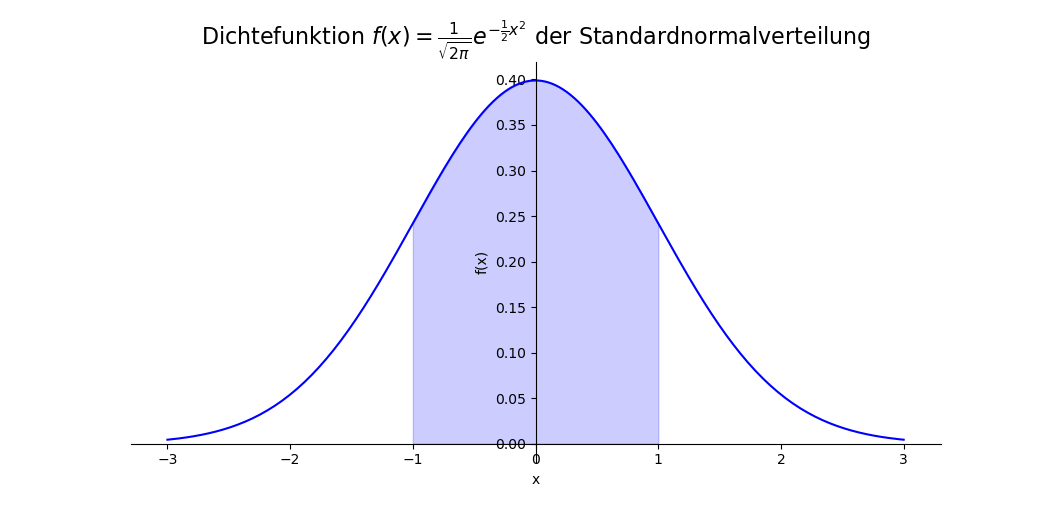
Auch für Stammfunktionen in Potenzreihenform gilt natürlich der Hauptsatz der Differential- und Integralrechnung. Somit ergibt sich \begin{eqnarray*} \int_{-1}^1 \frac{1}{\sqrt{2\pi}} \e^{-\frac{1}{2}x^2}\,dx & = & \frac{1}{\sqrt{2\pi}} \int_{-1}^1 \e^{-\frac{1}{2}x^2}\,dx \\[3mm] & = & \frac{1}{\sqrt{2\pi}} \left[ \sum_{n=0}^\infty \frac{(-1)^n x^{2n+1}}{(2n+1)2^n\,n!} \right]_{x=-1}^{x=1} \\[3mm] & = & \frac{1}{\sqrt{2\pi}} \left( \sum_{n=0}^\infty \frac{(-1)^n 1^{2n+1}}{(2n+1)2^n\,n!} - \sum_{n=0}^\infty \frac{(-1)^n (-1)^{2n+1}}{(2n+1)2^n\,n!} \right) \\[3mm] & = & \frac{1}{\sqrt{2\pi}} \sum_{n=0}^\infty \frac{(-1)^n (1-(-1))}{(2n+1)2^n\,n!} \\[3mm] & = & \frac{2}{\sqrt{2\pi}} \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)2^n\,n!} \end{eqnarray*}
Damit haben wir zumindest einen Wert des Integrals in Reihendarstellung, also als Grenzwert einer konvergenten Reihe.
Mithilfe dieser Reihendarstellung fällt es uns jetzt leicht, den Grenzwert approximativ zu berechnen. Dafür nutzen wir einfach die Summanden bis zu einer festen Stelle $n$. Wenn wir beispielsweise für die Reihe oben die ersten $15$ Summanden nehmen, also $n=0$ bis $14$, dann können wir mit dem folgenden Python-Programm das Integral schon bis zur Maschinengenauigkeit berechnen.
import math
sum = 0
for n in range(15):
sum = sum + ((-1) ** n) / ((2*n+1) * (2 ** n) * math.factorial(n))
sum = 2 / math.sqrt(2 * math.pi) * sum
print(sum)
Es ergibt sich \[ \int_{-1}^1 \frac{1}{\sqrt{2\pi}} \e^{-\frac{1}{2}x^2}\,dx \approx 0.682689492137086. \] Das Ergebnis ist bis auf $15$ Nachkommastellen genau.
Teilen und Drucken