Analysis
Graphentheorie
Analysis-Blog
Das Sandwich-Lemma
06 May 2024 13:22
Die Rechenregeln, die wir bisher für Grenzwerte kennen, basieren alle auf den arithmetischen Operationen. In dieser Blog-Folge zeige ich Dir eine ungleichungsbasierte Rechenregel für Grenzwerte. weiterlesen
Analysis-Blog
Folgen
27 May 2024 15:54
Von Intelligenztests kennen wir die Aufgabe, eine Abfolge von Zahlen passend fortzusetzen. weiterlesen
Analysis-Blog
Bestimmte Divergenz
06 May 2024 13:13
In dieser Blog-Folge wollen wir divergente Folgen genauer klassifizieren. weiterlesen
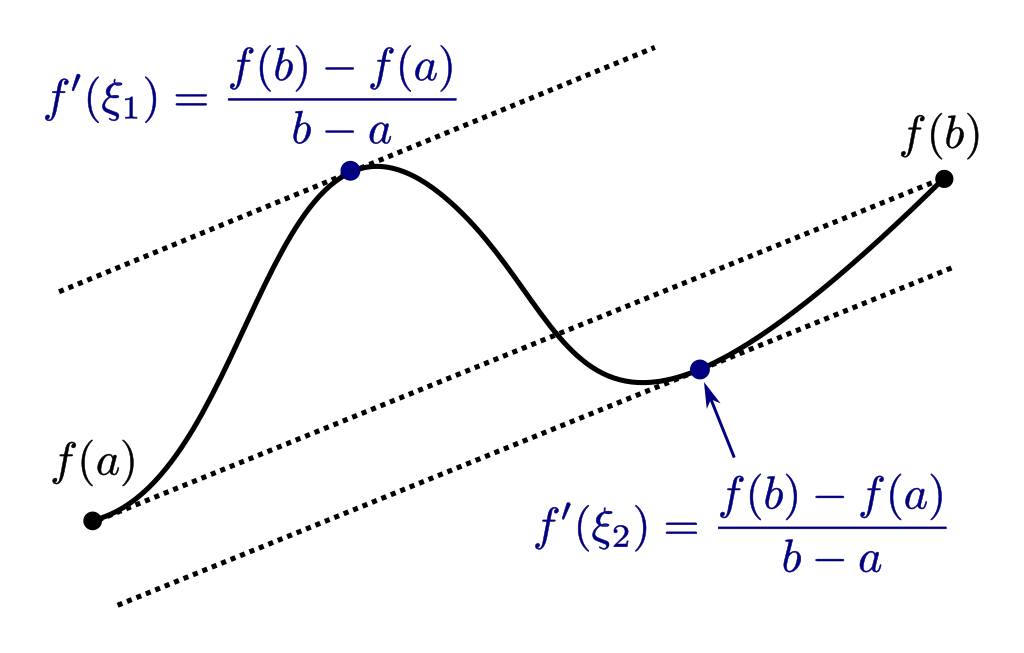
Analysis-Blog
Komplexen Zahlen als Vektoren
23 Apr 2024 09:33
Eine komplexe Zahl können wir als Punkt im $\mathbb{R}^2$ auffassen und somit auch als Vektor betrachten. In dieser Blog-Folge zeige ich Dir, wie die arithmetischen Operationen für komplexe Zahlen geomtrisch im $\mathbb{R}^2$ dargestellt werden können. weiterlesen
Analysis-Blog
Betrag und normierter Körper
10 Apr 2024 14:06
Aus der Linearen Algebra kennst Du den Begriff der Norm. Solch eine Norm ordnet den Vektoren eines Vektorraums eine nichtnegative Länge zu. Der analoge Begriff in Körpern ist der des Betrags. Durch eine Betragsfunktion wird jedem Körperelement eine nichtnegative Größe zugeordnet. In dieser Blog-Folge zeige ich Dir, wie man in einem angeordneten Körper solch eine Betragsfunktion definieren kann und welche wichtige Rechenregeln sich daraus ergeben. weiterlesen
Analysis-Blog
Übungen zu rekursiven Folgen
25 Apr 2024 09:27
Diese Blog-Folge enthält eine Reihe von Übungen zu Fibonacci-Zahlen und rekursiv definierte Folgen. weiterlesen
Analysis-Blog
Fakultät und Binomialkoeffizient
10 Apr 2024 11:34
Fakultät und Binomialkoeffizient sind Konzepte, die eigentlich aus der Kombinatorik stammen, die aber auch in der Analysis unverzichtbar ist. Beide sind wichtige Zählkoeffizienten, d. h. sie geben die Kardinalität bestimmter Mengen an. In dieser Blog-Folge lernen wir ihre Definition kennen. weiterlesen
Analysis-Blog
Sinus und Cosinus
27 May 2024 18:13
Neben der Exponentialfunktion sind Sinus und Cosinus zwei weitere elementare Funktionen der Mathematik. Sie basieren direkt auf der Exponentialfunktion. weiterlesen
Analysis-Blog
Die Wurzel aus 2 ist irrational
19 Apr 2024 16:12
Bisher haben wir die reellen Zahlen als angeordneten und normierten Körper konstruiert. Neben den reellen Zahlen gibt es aber auch andere Körper, die angeordnet und normiert sind, und die Du sogar schon kennst, beispielsweise den Körper $\mathbb{Q}$ der rationalen Zahlen. Wozu brauchen wir also noch die reellen Zahlen? In dieser Blog-Folge verrate ich Dir, welchen schweren Mangel die rationalen Zahlen haben. weiterlesen
Analysis-Blog
Die Fibonacci-Folge
25 Apr 2024 09:24
Folgen müssen nicht explizit definiert sein, sondern können auch rekurisv definiert werden. In der vorangegangenen Blogfolge haben wir bereits ein Beispiel hierfür gesehen. Die bekannteste rekursiv definierte Folge ist die Fibonacci-Folge. weiterlesen
Analysis-Blog
Intervallschachtelung
06 May 2024 16:19
In dieser Blog-Folge zeige ich Dir, was eine Intervallschachtelung ist. Mit ihr kann man konvergente Folgen konstruieren. weiterlesen
Analysis-Blog
Übung: Rechenregeln für einen angeordneten Körper
20 Apr 2024 09:04
Übung macht den Meister! Deshalb besteht diese Blog-Folge aus einer Reihe von Übungen. Sie bietet Dir damit die Gelegenheit, Deine Kenntnisse zu Körpern, angeordneten Körpern und Ungleichungen zu vertiefen. Bearbeite so viele Übungen wie möglich. weiterlesen
Analysis-Blog
Übungen zur Konvergenz von Reihen
27 May 2024 15:34
In den folgenden Übungen sollen Sie die Konvergenz von Reihen untersuchen oder Grenzwerte ermitteln. weiterlesen
Analysis-Blog
Binomischer Lehrsatz und Bernoullische Ungleichung
10 Apr 2024 11:57
In dieser Blog-Folge fragen wir uns, wie wir Potenzen von Binomen, also Ausdrücke der Form $(a+b)^n$, ausmultiplizieren können. Für $n=2$ kennst Du die Antwort bereits aus Deiner Schulzeit: $(a+b)^2$ multiplizierst Du mit der ersten binomischen Formel aus. Der binomische Lehrsatz verallgemeinert die erste und zweite binomische Formel auf ein beliebiges $n\in\mathbb{N}_0$. Dabei begegnen uns auch wieder die Binomialkoeffizienten. Zum Abschluss der Blog-Folge betrachten wir die Bernoullische Ungleichung. Mit ihr können wir die Potenz eines Binoms durch eine lineare Funktion nach unten abschätzen. weiterlesen
Analysis-Blog
Cauchy-Produkt
27 May 2024 15:52
Wir haben zwei Reihen die wir miteinander multiplizieren wollen. Das Produkt dieser Reihen soll dabei wieder als Reihe dargestellt werden. In dieser Blog-Folge zeige ich Dir, wie diese Reihendarstellung aussieht. weiterlesen
Analysis-Blog
Teleskopreihen
27 May 2024 15:13
In dieser Blog-Folge untersuchen wir die Reihe \[ \sum_{n=1}^\infty \frac{1}{n^2} \] auf Konvergenz. weiterlesen
Analysis-Blog
Übung: Vollständiger Körper
17 Apr 2024 12:12
Analysis-Blog
Übungen zur Partialbruchzerlegung
27 May 2024 19:06
Diese Blog-Folge bietet Dir die Gelegenheit, Partialbruchzerlegungen zu üben. weiterlesen
Analysis-Blog
Der Körper der reellen Zahlen
29 Mar 2024 16:26
Die Analysis, die wir in diesem Kurs behandeln, basiert in erster Linie auf den reellen Zahlen. Daher werden wir die reellen Zahlen im ersten Kapitel recht genau einführen. Wir beginnen damit, dass wir von den reellen Zahlen verlangen, dass sie einen Körper bilden. In diesem Zusammenhang werde ich den Begriff des Körpers und seine wichtigsten Eigenschaften kurz wiederholen. weiterlesen
Analysis-Blog
Vollständiger Körper
18 Apr 2024 08:41
Nachdem wir jetzt wissen, was ein Supremum ist, werden wir den Begriff in dieser Blog-Folge geschickt einsetzen. Unsere Absicht ist es, dafür zu sorgen, dass Gleichungen wie beispielsweise $x^2 = 2$ in den reellen Zahlen lösbar sind. Hier zeige ich Dir, wie uns dies gelingt. weiterlesen
Analysis-Blog
Reihen
27 May 2024 15:12
Reihen entstehen, indem wir die Folgenglieder einer Folge $(a_k)_{k\in \mathbb{N}_0}$ von $1$ bis $n$ aufsummieren. Die Summe dieser ersten $n$-Folgenglieder der Folge $(a_k)$ ergibt das $n$-te Folgenglied einer Reihe. weiterlesen
Analysis-Blog
Folgen in $\mathbb{C}$ und $\mathbb{R}^d$
06 May 2024 18:22
Bisher haben wir ausschließlich reelle Folgen behandelt. Aber natürlich können wir auch Folgen mit komplexen Zahlen als Folgenglieder definieren, ebenso Folgen, deren Folgenglieder Vektoren sind. In dieser Blog-Folge werden wir den Grenzwertbegriff auf solche Folgen ausdehnen. Du wirst feststellen, dass sich gegenüber dem Grenzwertbegriff für reelle Folgen praktisch nichts ändert. Auch viele weitere Aussagen, die wir für reelle Folgen formuliert und bewiesen haben, lassen sich auf komplexe Folgen übertragen. weiterlesen
Analysis-Blog
Cauchy-Folge
06 May 2024 18:13
Bei Cauchy-Folgen liegen die einzelnen Folgenglieder ab einem Index $n_0$ beliebig nahe beieinander. Wir werden sehen, dass dies äquivalent zur Konvergenz einer Folge ist, woraus ein weiteres Konvergenzkriterium entsteht. weiterlesen
Analysis-Blog
Die Komplexen Zahlen
17 Apr 2024 15:05
Die Einführung des Vollständigkeitsaxioms hat dafür gesorgt, dass wir in den reellen Zahlen die Gleichungen $x^k = a$ für positives $a$ lösen können. Dagegen hat die Gleichung $x^2 = -1$ keine Lösung in den reellen Zahlen. Dies wirft die Frage auf, ob wir die reellen Zahlen geeignet erweitern können, so dass $x^k = a$ auch für negative $a$ immer eine Lösung hat. weiterlesen
Analysis-Blog
Majoranten- und Minorantenkriterium
27 May 2024 15:20
Bei der Untersuchung einer Reihe auf Konvergenz kann es hilfreich sein, die Summanden der Reihe nach oben abzuschätzen, wenn durch die Abschätzung eine Reihe entsteht, deren Konvergenz bekannt ist. weiterlesen
Analysis-Blog
Absolute Konvergenz
27 May 2024 15:14
Wechselnde Vorzeichen bei den Summanden einer Reihe können die Untersuchung auf Konvergenz deutlich erschweren. Daher kann es von Bedeutung sein, bei der Untersuchung diese Vorzeichenwechsel zu ignorieren. weiterlesen
Analysis-Blog
Leibniz-Kriterium
27 May 2024 15:14
Eine alternierende Reihe ist eine Reihe in $\mathbb{R}$, bei der die Summanden ein wechselndes Vorzeichen haben. In dieser Blog-Folge lernst Du ein Konvergenzkriterium speziell für solche Reihen kennen. weiterlesen
Analysis-Blog
Wurzelkriterium
27 May 2024 15:29
Neben dem Quotientenkriterium, das wir im vorigen Blog behandelt haben, gibt es ein weiteres wichtiges Kriterium für die absolute Konvergenz von Reihen: das Wurzelkriterium. weiterlesen
Analysis-Blog
Noch mehr Übungen zur Konvergenz von Reihen
27 May 2024 15:38
In den folgenden Übungen sollen Sie die Konvergenz von Reihen untersuchen oder Grenzwerte ermitteln. weiterlesen
Analysis-Blog
Grenzwert einer Folge
19 Apr 2024 15:33
Der wichtigste Begriff der Analysis ist der des Grenzwerts. In dieser Blog-Folge werde ich den Begriff definieren und erläutern. Weiterhin betrachten wir erste Beispiele zum Nachweis der Grenzwerteigenschaft. weiterlesen
Analysis-Blog
Quotientenkriterium
27 May 2024 15:24
Aus dem Majorantenkriterium heraus kann man weitere spezialisierte Konvergenzkriterien entwickeln, deren Anwendung konkreter und damit üblicherweise etwas einfacher ist als das abstrakte Majorantenkriterium. weiterlesen
Analysis-Blog
Supremum
23 Apr 2024 12:53
Um den Mangel der rationalen Zahlen, dass beispielsweise die Gleichung $x^2 = 2$ in ihnen keine Lösung hat, zu beheben, werden wir eine zusätzliche Forderung an die reellen Zahlen stellen müssen, also ein weiteres Axiom aufstellen. Für die Formulierung dieses Axioms benötigen wir den Begriff des Supremums, den ich Dir in dieser Blog-Folge erkläre. weiterlesen
Analysis-Blog
Die Exponentialfunktion
27 May 2024 17:30
Die Exponentialfunktion gehört zu den wichtigsten Funktionen in der Mathematik. In dieser Blog-Folge schauen wir uns die Definition dieser Funktion auf Basis einer Potenzreihe und wichtige daraus resultierende Eigenschaften an. weiterlesen
Analysis-Blog
Übungen zu Potenzreihen und zum Cauchy-Produkt
27 May 2024 16:15
Die Ermittlung des Konvergenzradius für eine Potenzreihe ist eine typische Klausuraufgabe, wofür in Übung 2 eine Reihe von Beispielaufgaben bereit gestellt werden. Viele dieser Beispiele stammen auch aus Klausuren. weiterlesen
Analysis-Blog
Potenzreihen
27 May 2024 16:08
Wir kennen Polynome als Funktionen der Form \[ f(x) = a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n. \] Gilt $a_n \neq 0$, dann sagen wir, dass das Polynom den Grad $n$ hat. Wenn wir jetzt die Summation nicht bei $n$ stoppen sondern unendlich viele Terme der Form $a_k x^k$ betrachten, dann erhalten wir eine Potenzreihe. weiterlesen
Analysis-Blog
Eigenschaften und Rechenregeln konvergenter Folgen
06 May 2024 12:59
Nach dem wir nun wissen, was ein Grenzwert einer Folge ist, stellt sich die Frage, ob es Rechenregeln für solche Grenzwerte gibt und wie diese aussehen. Konkret: Wenn wir zwei konvergente Folgen $(a_n)$ und $(b_n)$ haben, mit den Grenzwerten $a$ bzw. $b$, ist dann auch die Folge $(a_n + b_n)$ konvergent? Und wenn ja, wie sieht deren Grenzwerte aus? Und wie ist dies für andere arithmetische Operationen, also z. B. für die Folge $(a_n b_n)$? weiterlesen
Analysis-Blog
Partialbruchzerlegung
27 May 2024 19:05
Mit der Partialbruchzerlegung können wir einen Quotienten von Polynomen in eine Summe einfacherer Terme zerlegen. weiterlesen
Analysis-Blog
Der Identitätssatz für Potenzreihen
27 May 2024 19:00
Kann es verschiedene Potenzreihen geben, die die gleiche Funktion darstellen? Der Identitätssatz für Potenzreihen liefert die Anwort auf diese Frage. weiterlesen
Analysis-Blog
Sinus Hyperbolicus und Cosinus Hyperbolicus
27 May 2024 18:51
In dieser Blog-Folge definieren wir die elementaren Hyperbelfunktionen, den Sinus Hyperbolicus und den Cosinus Hyperbolicus, mithilfe der Exponentialfunktion. weiterlesen
Analysis-Blog
Rechenregeln für einen angeordneten Körper
10 Apr 2024 11:12
In der vorigen Blog-Folge hatten wir definiert, was ein angeordneter Körper ist. In solch einem Körper können wir nicht nur mit den bekannten arithmetischen Operation $+$ und $\cdot$ rechnen, sondern wir können auch Ungleichungen aufstellen. In dieser Blog-Folge werden wir weitere Rechenregeln für Ungleichungen herleiten. weiterlesen
Analysis-Blog
Übungen zur Herleitung expliziter Formeln für Folgen
28 May 2024 08:05
In dieser Blog-Folge findest Du verschiedene Übungen zur Herleitung expliziter Formeln für rekursiv definierte Folgen. weiterlesen
Analysis-Blog
Herleitung der Formel von Moivre-Binet
28 May 2024 07:57
In dieser Blog-Folge zeige ich Dir, wie Du mit den gelernten Techniken die bekannte Formel von Moivre-Binet zur expliziten Darstellung der Fibonacci-Zahlen herleiten kannst. weiterlesen
Analysis-Blog
Explizite Formeln für Folgen
28 May 2024 07:51
Nachdem wir in den vorigen Blog-Folgen (siehe hier und hier) den Identitätssatz für Potenzreihen kennengelernt und uns mit der Partialbruchzerlegung vetraut gemacht haben, sind wir nun soweit, dass wir für rekursiv definierte Folgen eine explizite Formel herleiten können. weiterlesen
Analysis-Blog
Kriterium der monotonen Konvergenz
06 May 2024 13:33
Um die Konvergenz einer Folge nachzuweisen, stehen uns bisher die Grenzwertdefinition und Rechenregeln für Grenzwerte zur Verfügung. Häufig können wir den Grenzwert einer Folge aber nicht benennen, d. h. wir vermuten, dass eine Folge konvergent ist, wissen aber nicht, welcher Zahl sich die Folgenglieder annähern. In dieser Blog-Folge wirst Du ein erstes Kriterium kennenlernen, mit dem Du nachweisen kannst, dass eine Folge konvergent ist, ohne ihren Grenzwert zu kennen. weiterlesen
Analysis-Blog
Angeordneter Körper
29 Mar 2024 15:43
In der Analysis benötigen wir nicht nur Gleichungen, sondern auch Ungleichungen spielen eine ganz entscheidende Rolle. Daher sollten wir in der Lage sein, auch mit Ungleichungen zu rechnen. Solche Ungleichungen basieren auf einer Anordnung der Körperelemente. In dieser Blog-Folge schauen wir uns an, wie solch ein angeordneter Körper charakterisiert ist. weiterlesen
Analysis-Blog
Übungen zu Fakultät, Binomialkoeffizient, Binomischer Lehrsatz, Bernoullische Ungleichung und Betrag
20 Mar 2024 14:16
Eine weitere Blog-Folge, die nur Übungen und die zugehörigen Musterlösungen enthält. Ideal, um deine Kenntnisse zu normierten Körpern zu vertiefen. weiterlesen
Analysis-Blog
Übung zu Komplexen Zahlen
26 Mar 2024 15:11